3  Beschrijvende statistiek

Doelstellingen

Bij wat de beschrijvende statistiek genoemd wordt, gaat het om het beschrijven van een gegevensverzameling door de gegevens te ordenen, samen te vatten en weer te geven op een informatieve manier. Dit kan in numerieke vorm door een aantal statistieken (samenvattende getallen) te berekenen, maar ook in grafische vorm. Hierdoor ben je sneller in staat om de gegevensverzameling te begrijpen. Welke vorm je gebruikt hangt vooral af van de gewenste informatie over de gegevens. Bij het gebruik van de verschillende technieken moet je een onderscheid maken tussen categoriale variabelen en numerieke variabelen.

3.1 Ordening Categoriale variabelen

Voor categoriale variabelen kun je geen zinvolle statistieken als gemiddelde, minimum of maximum bepalen. Wel kun je samenvattingen maken door de frequenties van de waarden te tellen. In Excel gaat dit het handigste met draaitabellen. Naast absolute aantallen voor elke categorie (frequenties) kun je ook percentages voor elke categorie weergeven (relatieve frequenties). Verschillen tussen categorieën zijn hierdoor snel zichtbaar.

3.1.1 Frequentietabel

Taak 3.1 Hulpbestand: vakanties.xlsx

Aan 200 personen van drie verschillende leeftijdsklasses (jong, middelbaar, oud) is gevraagd wat hun favoriete vakantieland (Griekenland, Spanje, Turkije, Italië) is.

  1. Open het bestand vakanties.xlsx en plaats de cursor ergens in de dataset en zet deze om naar een Excel tabel via tab Invoegen > Tabel.

  2. Kies daarna tab Invoegen > Draaitabel en laat deze in een nieuw werkblad plaatsen.

  3. Om de frequenties van de vakantielanden te bepalen sleep je het veld Vakantieland naar de Rijen en het veld id naar de Waarden. Standaard maakt Excel daar Som van id van. Dit is niet goed.

  4. Klik op het keuzepijltje in het vak Som van id en kies Waardeveldinstellingen. Onder Waardeveld samenvatten op selecteer je Aantal.

  5. Wijzig verder de Aangepaste naam in Aantal en daarna OK.

  6. Om ook de relatieve frequenties weer te geven sleep je het veld id nogmaals naar de Waarden, onder Aantal. Excel maakt er weer Som van id van. Wijzig dit analoog aan het voorgaande weer in samenvatten op Aantal.

  7. Daarna selecteer je in hetzelfde dialoogvenster de tab Waarden weergeven als en wijzig je de standaardkeuze Geen berekening in % van eindtotaal.

  8. Pas tot slot de naam van de kolom aan in Percentage en klik dan OK.

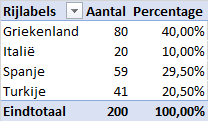
Figuur 3.1: Frequenties favoriete vakantielanden.

Sluit de werkmap nog niet want je hebt deze nog nodig voor de volgende oefening.

3.1.2 Kruistabel

Om een verband tussen twee categoriale veriabelen te onderzoeken gebruik je een kruistabel. Hierin staan de categorieën van de ene variabele (de rijvariabele) in de rijen en de categorieën van de andere variabele (de kolomvariabele) in de kolommen. In de cel waar een rijwaarde en een kolomwaarde elkaar kruisen staat het aantal dat tot beide categorieën behoort.

Behalve als aantal (= frequentie) kunnen de tellingen ook worden weergegeven als een percentage van het totale totaal, van het rijtotaal of van het kolomtotaal. Door deze weergave kun je patronen bestuderen die tussen de variabelen kunnen bestaan. Kruistabellen maak je ook het beste maken met draaitabellen.

Taak 3.2 Hulpbestand: vakanties.xlsx

Maak een kruistabel van de variabelen Leeftijdsklasse en Vakantieland.

  1. Maak je een nieuwe draaitabel.

  2. Sleep het veld Leeftijdsklasse naar de Rijen, het veld Vakantieland naar de Kolommen en het veld id naar de Waarden.

  3. Wijzig de Waardeveldinstellingen weer in Aantal in plaats van Som.

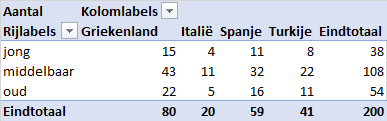
Figuur 3.2: Kruistabel van Leeftijdsklasse met Vakantieland.

Visualisatie met een kolomdiagram.

  1. Selecteer en veld in de draaitabel en kies dan Invoegen > Gegroepeerde kolom (groep Grafieken).
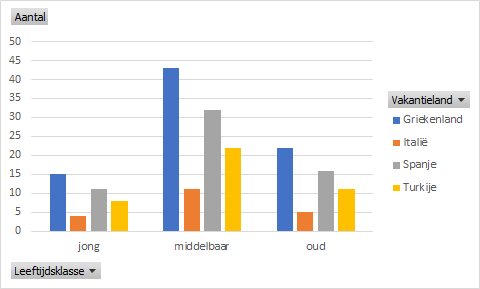
Figuur 3.3: Kolomdiagram van Vakantieland per Leeftijdsklasse.

Uiteraard kun je dit standaarddiagram nog op de bekende manieren verder verfraaien.

3.2 Ordening kwantitatieve variabelen

Wanneer het aantal waarnemingen van een kwantitatieve variabele niet al te groot is kun je een beter gevoel voor de data krijgen door deze te ordenen (sorteren) van klein naar groot. Je ziet dan snel het bereik van de waarden. Bij een groter aantal data kun je beter van een frequentietabel gebruik maken.

3.2.1 Frequentieverdelingen

Bij een frequentieverdeling van een kwantitatieve variabele wordt het bereik van de waarden opgedeeld in een aantal geordende klassen en geteld hoeveel waarden in elke klasse voorkomen. De grenzen van een klasse, de ondergrens en bovengrens, worden met een combinatie van ronde haken () en blokhaken [] aangeduid. Een ronde haak betekent dat de grenswaarde niet tot de klasse behoort. Een blokhaak betekent dat de grenswaarde wel tot de klasse behoort. Zo hoort bij een klasse aangeduid met [25,40) de waarde 25 wel tot de klasse, maar de waarde 40 niet.

De klassebreedte is het verschil tussen de bovengrens en de ondergrens van een klasse. Zo heeft de klasse [25,40) een klassebreedte 15. Om een bruikbare frequentieverdeling te maken moet je een beslissing nemen over het aantal klassen en dus over de klassebreedte. Bij teveel of te weinig klassen kun je weinig informatie uit de frequentieverdeling halen. In de praktijk zie je vaak 5 tot 15 klassen.

Voor het maken van klassen (bins geheten in Excel) gelden de volgende regels:

  • De klassen mogen geen overlappingen vertonen. Een waarneming moet slechts in één klasse ondergebracht kunnen worden. Een indeling met hierin de klassen [25,50] en [50,75] kan dus niet. Want dit zou inhouden dat de waarde 50 tot 2 klassen kan behoren.

  • Voor elke waarneming moet er een klasse beschikbaar zijn. Dus alle waarnemingen moeten in een klasse ondergebracht kunnen worden. Vaak worden daarom de eerste en laatste klasse extra groot gemaakt.

  1. Als het kan maak dan de klassen even breed. Excel kan hier beter mee overweg dan wanneer de klassen niet even breed zijn. Voor de eerste en de laatste klasse lukt dat niet alijd omdat alle waarnemingen opgevangen moeten worden. Daarnaast kunnen er ook andere redenen zijn om de klassen niet even breed te maken. Ook worden soms klassen waarin weinig waarnemingen zitten samengevoegd waardoor een bredere klasse ontstaat.

  2. De klassen moeten wel voldoende differentieren (verschillen vertonen) anders levert de frequentieverdeling te weinig informatie op. Zo heeft het weinig zin om voor de inkomensverdeling in Nederland een klasse van €10.000 tot €60.000 te maken, omdat hierin bijna alle inkomens (> 90%) vallen.

Relatieve frequentieverdeling

De relatieve frequenties worden uitgedrukt als fracties of als een percentages. Deze verdeling kun je het beste via draaitabellen maken.

Cumulatieve frequentieverdeling

De cumulatieve frequentie is de som van alle frequenties tot en met de frequentie van de desbetreffende waarde. Met name wanneer je gebruik maakt van percentages heb je een manier om te laten zien welk percentage waarden kleiner is dan een bepaalde waarde.

3.2.2 Functie INTERVAL

Syntax: INTERVAL(gegevensmatrix;interval_verw)

Het eerste argument is de matrix met de waarden waarvan je de frequenties wilt bepalen. Het tweede argument is de matrix met de bovengrenzen van de klassen (de intervallen).

Om een frequentieverdeling van de gegevens te maken moet je als voorbereiding eerst de intervallen (bins) vaststellen waarin de waarden moeten vallen. Hiervoor maak je een kolom met de bovengrenzen van de intervallen.

Taak 3.3 Hulpbestand: frequenties.xlsx

  1. Open het bestand frequenties.xlsx en daarin het werkblad data. De gegevens in de kolom getal zijn 25 willekeurige gehele getallen uit het interval [1,10].
  2. Typ in cel C1 de tekst bin en in de cellen C2 t/m C6 de getallen 2,4,6,8,10. Dit zijn de bovengrenzen van de intervals.
  3. Typ in cel D1 de tekst frequentie.
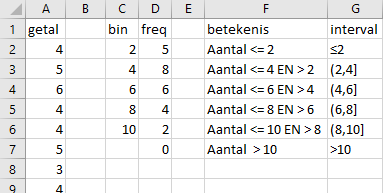
  4. Selecteer cel D2 en voer de volgende formule in: =INTERVAL(A2:A26;C2:C6).

Deze formule is een zogenaamde matrixformule. Je kunt deze matrixformule gewoon in de begincel D2 invoeren en vervolgens op Enter drukken. Het resultaat is een kolommetje getallen, een matrix. Excel weet welke cellen nodig zijn voor de uitvoer en plaatst het resultaat van deze dynamische matrix in deze cellen. Deze cellen moeten wel leeg zijn anders krijg je een foutmelding.

Het resultaat van de intervalformule is te zien in Figuur 3.4. Om duidelijk te maken wat nu de gebruikte intervallen zijn is in de kolommen F en G een toelichting toegevoegd.

Sluit de werkmap nog niet want je hebt deze nog nodig voor de volgende oefening.

Figuur 3.4: Frequenties bepaald met functie INTERVAL.

3.2.3 Draaitabel methode

Taak 3.4 Hulpbestand: frequenties.xlsx

  1. Selecteer in het bestand frequenties.xlsx het gegevensgebied A1:A26 en kies dan tab Invoegen > Draaitabel en laat deze in een nieuw werkblad plaatsen.

  2. Plaats het veld getal in zowel het rijengebied als het waardengebied. Wijzig daarna de waardeveldinstellingen zodat het aantal bepaald wordt en niet de som.

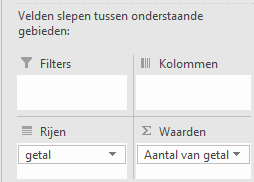
Figuur 3.5: Velden voor de draaitabel.

Nu moet er nog gegroepeerd worden voor de intervals.

  1. Selecteer een willekeurig veld in de draaitabel, rechter muisklik > Groeperen.

  2. Stel in het dialoogscherm in dat wordt begonnen bij 1, geeindigd bij 10 en dat de stapgrootte 2 is. Na het groeperen verschijnt de frequentieverdeling.

Figuur 3.6: Frequentieverdeling via een draaitabel.
  1. Bewaar het bestand, je hebt het nog nodig voor een volgende oefening.

Een frequentieverdeling kun je in Excel ook maken met de histogram optie in de addin Gegevensanalyse. Deze methode komt in Paragraaf 3.4.1 aan bod.

Welke manier je in de praktijk gebruikt hangt meestal af van de gewenste uitvoer en de mogelijkheden tot het maken van aanpassingen.

3.3 Numerieke statistieken

Voor variabelen kun je samenvattende grootheden maken, statistieken geheten, zoals wat het centrum van de gegevens is en hoe de gegevens verspreid zijn.

3.3.1 Centrum dataset

Bij een analyse is het van belang om te weten bij welke waarde het grootste deel van de gegevens zitten. Dit is het centrum van de dataset. De meest gebruikte maten hiervoor zijn gemiddelde en mediaan. En wat minder de modus. Welke maat het meest geschikt is om het centrum te bepalen hangt van de situatie en het meetniveau van de variabele af.

  • gemiddelde - geschikt voor symmetrische verdelingen zonder uitschieters.
  • mediaan - geschikt voor scheve verdelingen of data met uitschieters
  • modus - geschikt voor categoriale variabelen

Gemiddelde

Voor een populatie wordt het gemiddelde aangegeven met het symbool \(\mu\) en berekend door de som van alle waarnemingen te delen door het totaal aantal waarnemingen. Doordat alle waarnemingen meetellen bij het bepalen van het gemiddelde hebben uitschieters grote invloed. Wanneer er extreme waarden voorkomen kun je beter een andere maat voor het centrum gebruiken.

Excel formule: GEMIDDELDE(data)

Mediaan

De mediaan is de middelste waarneming van een van klein naar groot gesorteerde reeks. Deze splitst dus de verzameling in twee helften: de laagste 50% en de hoogste 50%. Bij een oneven aantal is de mediaan de middelste waarneming. Bij een even aantal zijn er twee waarden die het midden vormen en neem je het gemiddelde van deze twee waarden. Uitschieters hebben geen invloed op de mediaan, waardoor de mediaan een goed alternatief is voor het gemiddelde wanneer er extreme waarden aanwezig zijn.

Excel formule: MEDIAAN(data)

Modus

De modus is de waarde die het meest voorkomt in de reeks. Uitschieters hebben geen invloed op de modus. Wanneer er meerdere waarden zijn met de hoogste frequentie dan is er eigenlijk geen modus. Excel heeft wel een formule om in dat geval de waarden met de hoogste frequentie te bepalen.

Excel formules:

  • MODUS.ENKELV(data) - Geeft de meest voorkomende waarde
  • MODUS.MEERV(data) - Geeft een verticale matrix van de meest voorkomende waarden
  • MODUS(data) - Verouderd, geeft dezelfde resultaten als MODUS.ENKELV()

Testvragen

Typ bij de volgende vragen het antwoord in het vakje. Voor eventuele decimalen moet je een punt gebruiken en geen komma!

  1. Een dataset bestaat uit de volgende verzameling getallen: [8, 2, 3, 15, 8, 6, 0]

    • Wat is de modus?
    • Wat is de mediaan?
    • Wat is het gemiddelde?

  2. Een dataset bestaat uit de volgende verzameling tien getallen: [1, 2, 2, 4, 5, 7, 7, 9, 9, 9]

    • Wat is de modus?
    • Wat is de mediaan?
    • Wat is het gemiddelde?

  3. Welke centrummaat kun je toepassen bij nominale data?

  4. In een normale verdeling zijn gemiddelde, mediaan en modus .

3.3.2 Spreiding dataset

Het bepalen van het centrum geeft slechts gedeeltelijke informatie over een dataset. Het is ook belangrijk om te kijken naar de spreiding. Deze geeft aan hoe erg de meetwaarden van elkaar verschillen en verwijderd zijn van het centrum.

Variantie en Standaarddeviatie

De meest gebruikte maten om de spreiding van de gegevens weer te geven zijn variantie en standaarddeviatie. Voor een populatie wordt de variantie weergegeven met het symbool \(\sigma^2\) en de standaarddeviatie met \(\sigma\).

De variantie en standaarddeviatie worden berekend met de volgende formules:

\[variantie (\sigma^2) = \frac{1}{N}\sum_{i=1}^{N}{(x_i- \mu)}^2\]

Van alle waarnemingen (\(x_i\)) wordt het verschil met het gemiddelde (\(\mu\)) gekwadrateerd. En de som van deze kwadraten wordt gedeeld door het totaal aantal waarnemingen (\(N\)). Je berekent dus in feite het gemiddelde van de kwadratische afwijkingen.

Voor de standaarddeviatie (standaardafwijking) geldt:

\[standaarddeviatie (\sigma) = \sqrt{variantie}\]

Zowel de variantie als de standaarddeviatie kunnen nooit negatief zijn.

Bij een steekproef met \(n\) waarnemeningen uit de populatie wordt de variantie aangeduid met \(s^2\) en berekend via \(s^2 = \frac{1}{n-1}\sum_{i=1}^{n}{(x_i- \bar{x})}^2\), waarbij \(\bar{x}\) het steekproefgemiddelde is.

Excel formules:

  • VAR.P(data) - Variantie voor een populatie
  • VAR.S(data) - Variantie voor een steekproef
  • STDEV.P(data) - Standaarddeviatie voor een populatie
  • STDEV.S(data) - Standaarddeviatie voor een steekproef
  • DEV.KWAD(data) - Som kwadratische afwijkingen

Kwartielen

Je kunt een gesorteerde reeks ook in vier gelijke stukken verdelen, elk met 25% van de waarnemingen. Deze heten dan kwartielen. Het eerste kwartiel \(Q_1\) splitst de verzameling in de laagste 25% en de hoogste 75%, Het tweede kwartiel \(Q_2\) is gelijk aan de mediaan. En het derde kwartiel \(Q_3\) splitst de verzameling in de laagste 75% en de hoogste 25%. Verder is \(Q_0\) gelijk aan de minimumwaarde en is \(Q_4\) gelijk aan de maximumwaarde.

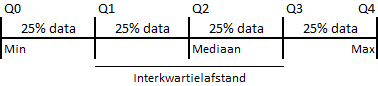
Figuur 3.7: Schematische weergave van de verdeling van een dataset in kwartielen.

De afstand tussen het eerste kwartiel \(Q_1\) en het derde kwartiel \(Q_3\) heet de interkwartielafstand.

Er zijn verschillende manieren waarop de kwartielen precies berekend worden, waardoor er kleine verschillen kunnen ontstaan tussen de verschillende applicaties. Veel applicaties splitsen de gegevens in twee helften en bepalen dan de mediaan van elke helft. Excel doet dat niet en berekent kwartielen via percentielen.

Excel formules:

  • KWARTIEL.INC(data;kwartiel) - Bepaling kwartiel (0,1,2,3,4) waarbij alle waarden meetellen, kun je het beste gebruiken.
  • KWARTIEL.EXC(data;kwartiel) - Bepaling kwartiel (1,2,3) waarbij de uiterste waarden niet meegeteld worden
  • KWARTIEL(data;kwartiel) - Verouderd, geeft dezelfde waarden als KWARTIEL.INC()

5-getallensamenvatting

Hiermee wordt bedoeld een opsomming van de waarden \(Q_0\), \(Q_1\), \(Q_2\), \(Q_3\) en \(Q_4\). Je krijgt dan een beknopte samenvatting die je inzicht geeft in het centrum, de spreiding en het bereik van de gegevens.

Spreidingsbreedte

De spreidingsbreedte is het verschil tussen de grootste en de kleinste waarneming. Deze maat is eenvoudig uit te rekenen, maar wel erg gevoelig voor extreme waarden (uitbijters).

Excel formule: MAX(data) - MIN(data)

Gemiddelde absolute afwijking

Dit is het gemiddelde van de absolute waarden van het verschil van een waarneming met het gemiddelde.

Excel formule: GEM.DEVIATIE(data)

Interkwartielafstand

Dit is het verschil tussen het derde kwartiel en het eerste kwartiel, dus \(Q_3 - Q_1\). Het is een manier om de spreiding van de middelste 50% van de gegevens weer te geven.

Excel formule: KWARTIEL(data;3) - KWARTIEL(data;1)

Variatiecoëfficient

De variatiecoëfficient (VC) is de standaarddeviatie gedeeld door het gemiddelde.

\(VC = \frac{\sigma}{\mu}\) (voor een populatie), \(VC = \frac{s}{\bar{x}}\) (voor een steekproef)

De variatiecoëfficient wordt vaak als een percentage uitgedrukt. Je kunt er mee aangeven of de standdardeviatie groot of klein is ten opzichte van het gemiddelde. Een kleine variatiecoefficient geeft aan dat de waarden slechts weinig fluctueren rond het gemiddelde. De variatiecoëfficiënt wordt vaak gebruikt om de variatie tussen twee verschillende datasets te vergelijken.

3.3.3 Z scores

Wanneer twee datsets verschillende gemiddelden en verschillende standaardwaarden hebben kun je niet zomaar een waarde uit de ene dataset vergelijken met een waarde uit een andere dataset. Om ze wel te kunnen vergelijken moet je de waarden in de datasets eerst standaardiseren door de waarden om te zetten in zogenaamde z-waarden of z-scores.

De z-score van een waarde is het verschil tussen die waarde en het gemiddelde, gedeeld door de standaarddeviatie:

\(z = \frac{x - \mu}{\sigma}\)

Het gemiddelde zelf heeft een z-score van 0. Waarden groter dan het gemiddelde hebben een positieve z-score en waarden kleiner dan het gemiddelde een negatieve z-score. De z-score geeft in feite aan hoeveel keer de standaaarddeviatie een waarde van het gemiddelde af ligt.

Via de z-scores kun je ook gemakkelijker eventuele uitschieters opsporen. Een vuistregel is dat een waarde met een z-score kleiner dan -3 of groter dan 3 als een uitschieter beschouwd kan worden.

Excel formule: NORMALISEREN(x ; gemiddelde ; standaarddeviatie)

Voor het gebruik hiervan moet je wel eerst het gemiddelde en de standaarddeviatie berekenen of een formule hiervoor opnemen.

3.3.4 Scheefheid en Kurtosis

Scheefheid en kurtosis zijn twee belangrijke maatstaven in de statistieken. Scheefheid verwijst naar het gebrek aan symmetrie en kurtosis verwijst naar de piek van een verdeling.

Scheefheid

Kenmerken van een scheve verdeling zijn:

  • Gemiddelde, mediaan en modus vallen op verschillende punten.
  • Kwartielen liggen niet op gelijke afstand van de mediaan.
  • De curve is niet symmetrisch zoals bij een normale verdeling, maar meer naar de ene kant uitgerekt dan naar de andere, heeft een staart.

Bij een frequentieverdeling kun je drie vormen van de curve aantreffen.

  1. Symmetrische verdeling

  2. Rechts scheve verdeling - Heeft een lange rechterstaart, wat duidt op extreme waarden aan de positieve kant van de verdeling.

  3. Links scheve verdeling - Heeft een lange linkerstaart, wat duidt op extreme waarden aan de negatieve kant van de verdeling.

Figuur 3.8: Scheve verdelingen.

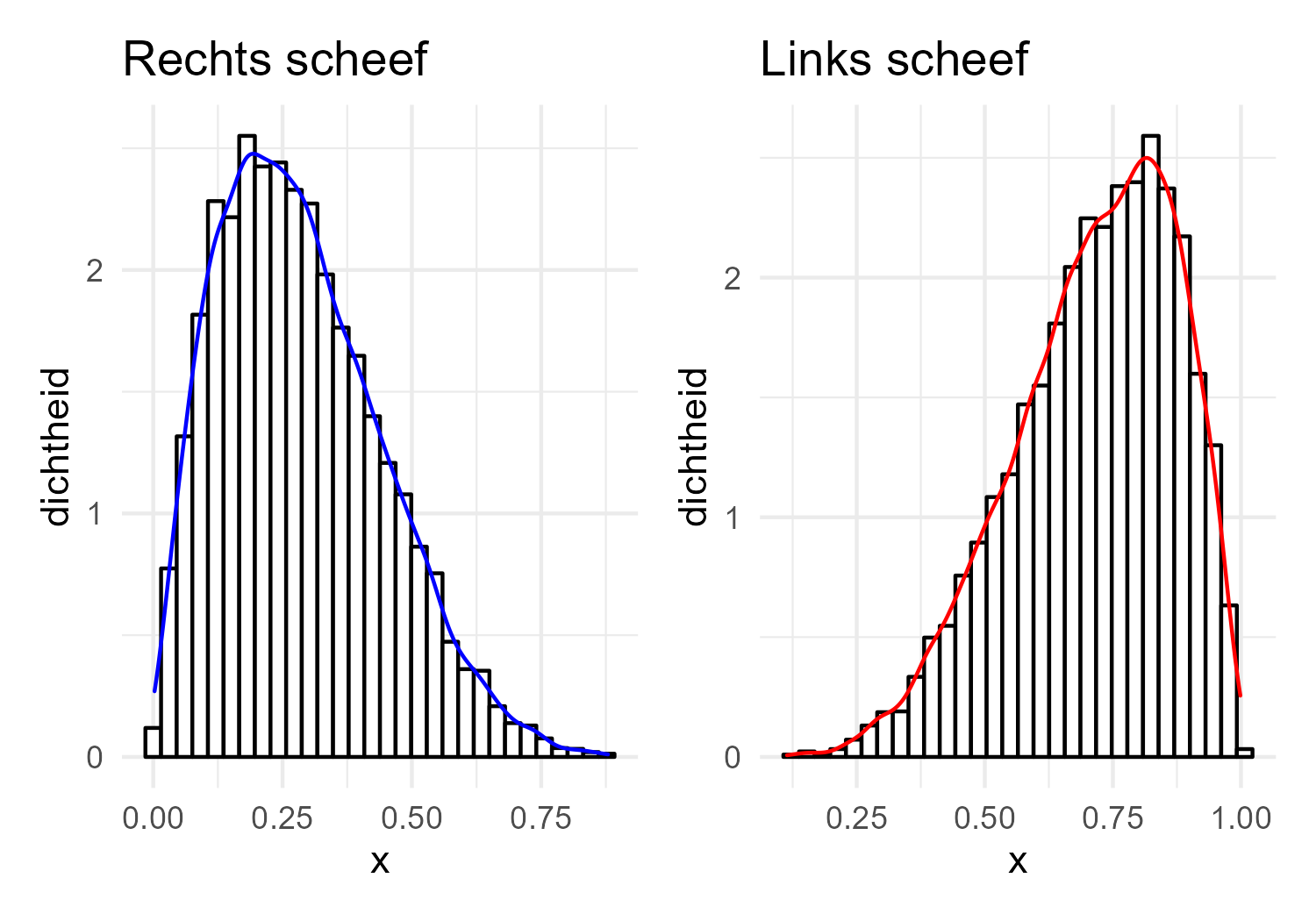
Kurtosis

Kurtosis is een statistische maatstaf die aangeeft in welke mate de data zich in de staarten of de piek van een verdeling bevinden. Vergeleken met een normale verdeling kunnen verdelingen een negatieve of een positieve kurtosis hebben.

  • Positieve kurtosis - Verdeling heeft een scherpere piek en heeft zwaardere staarten, wat wijst op meer uitschieters en minder waarden in de buurt van het gemiddelde.

  • Negatieve kurtosis - Verdeling is minder gepiekt en heeft dunnere staarten, wat wijst op minder uitschieters en meer waarden in de buurt van het gemiddelde.

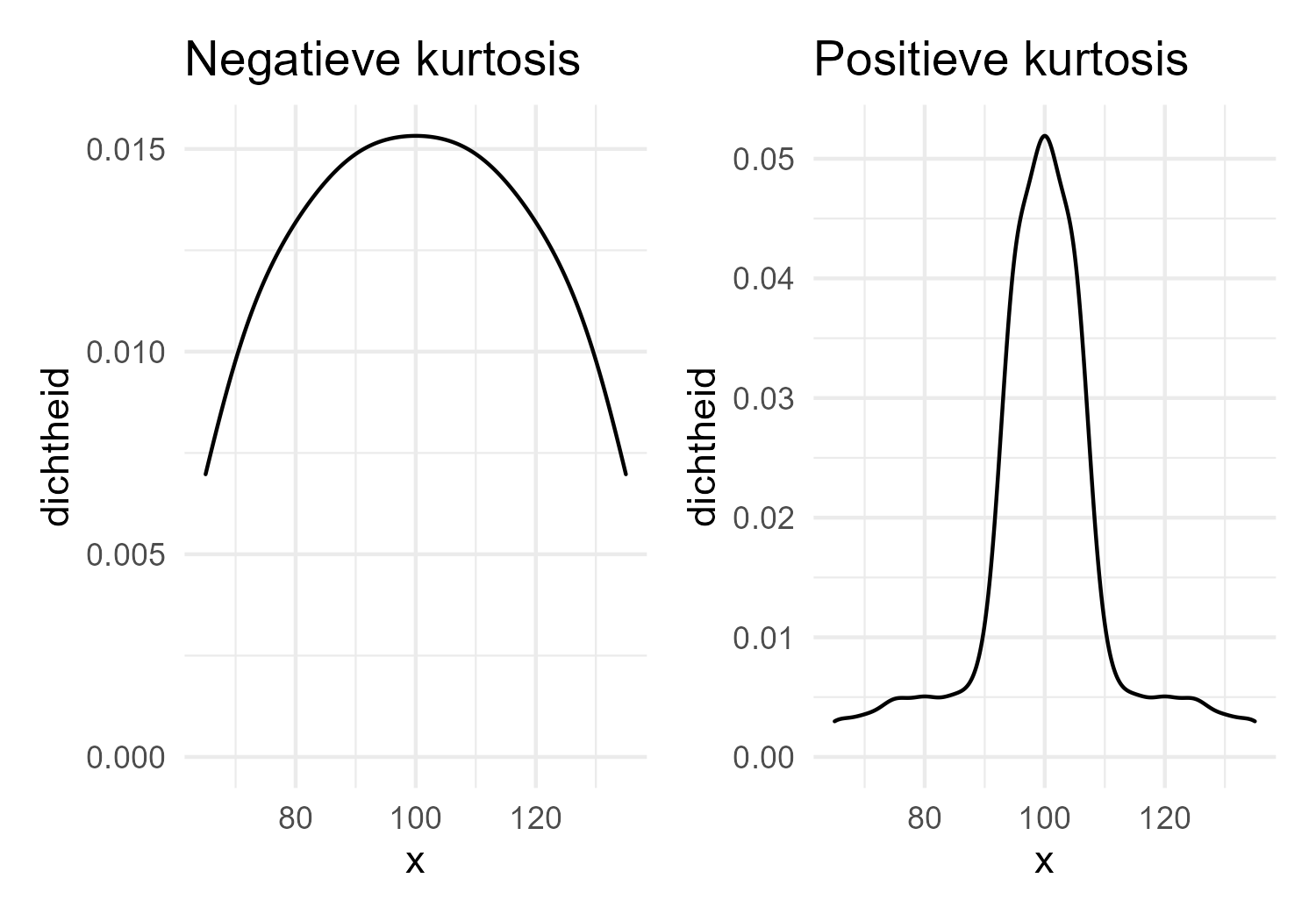
Figuur 3.9: Dichtheidsdiagram voor verdelingen met een negatieve en positieve kurtosis.

Bij data-analyse is het concept van kurtosis belangrijk bij het onderzoeken van mogelijke relaties tussen variabelen. Bij een variabele met een hoge kurtosis liggen de waarden dicht bij elkaar (vandaar de piek) en is de kans op een relatie met andere variabelen klein.

In de financiële wereld wordt op het gebied van risicobeheer en beleggingsrendement vaak gekeken naar de kurtosis. Deze geeft aan of er enige kans is op extreme waarden van rendementen.

Excel formules

Er zijn verschillende formules om de scheefheid en kurtosis in een getal uit te drukken. Je kunt hier echter weinig mee. Het is beter om naar de frequentieverdeling te kijken.

  • SCHEEFHEID(data)
  • SCHEEFHEID.P(data) voor een populatie
  • KURTOSIS(data)

3.4 Grafieken

Grafieken zijn een onmisbaar hulpmiddel bij de analyse van gegevens. Veel gebruikte grafieksoorten zijn kolom/staaf diagram, lijndiagram, spreidingsdiagram, histogram, boxplot. De laatste twee soorten worden hier verder besproken, de andere grafieksoorten worden als bekend verondersteld.

3.4.1 Histogram

Een histogram is een grafische weergave van de frequentieverdeling van een kwantitatieve variabele in de vorm van een kolomdiagram. De waarden van de variabelen worden in een vooraf gedefinieerd aantal delen (bins) verdeeld, die fungeren als containers voor de waarden. Het aantal waarden in elke bin zijn dan de frequenties.

Een histogram kan antwoord geven op de volgende vragen:

  • Van wat voor soort verdeling zijn de gegevens afkomstig?
  • Waar bevinden de gegevens zich?
  • Hoe verspreid zijn de gegevens?
  • Zijn de gegevens symmetrisch of scheef?
  • Zijn er uitschieters in de gegevens?

Excel heeft twee mogelijkheden voor het genereren van een histogram:

  • via invoegtoepassing Gegevensanalyse (voor activering zie Bijlage A)
  • via grafiektype histogram.

Via Gegevensanalyse

Ook voor deze methode moet er net als bij de functie INTERVAL() eerst handmatig een bereik voor de grenzen van de intervallen gemaakt zijn.

Taak 3.5 Hulpbestand: frequenties.xlsx

  1. Open in het eerder gebruikte bestand frequenties.xlsx het werkblad data.
  2. Kies dan tab Gegevens > Gegevensanalyse > Histogram.
  3. Specificeer het invoerbereik, het verzamelbereik, uitvoer op een nieuw werkblad en selecteer Grafiek maken.
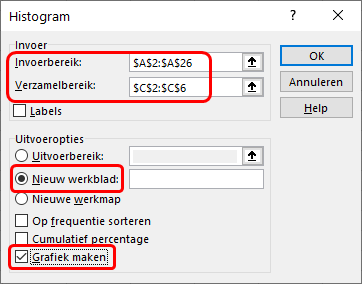
Figuur 3.10: Specificaties voor frequentietabel en histogram.
  1. Klik OK en daarna verschijnt het resultaat in een nieuw werkblad.
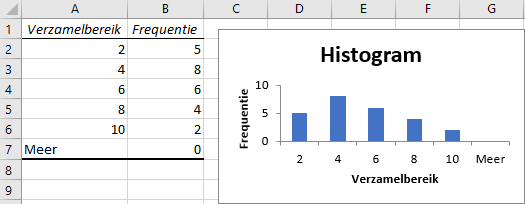
Figuur 3.11: De frequentietabel met histogram.
  1. Bewaar het bestand, je hebt het nog nodig voor een volgende oefening.

De grafiek is een gegroepeerde kolomdiagram die je desgewenst nog kunt aanpassen. Voor een echt histogram moeten de kolommen aansluitend zijn zonder lege ruimte ertussen. En de labels op de X-as geven hier alleen de bovengrens van het interval en niet het interval zelf.

De frequentieverdeling en histogram zijn statisch. Wanneer de brondata wijzigt vindt er geen herberekening plaats.

Via grafiektype histogram

De nieuwere Excelversies hebben de mogelijkheid tot het invoegen van een grafiektype Histogram. Hiervoor heb je in principe alleen maar de brondata nodig. De verdeling in intervallen (bins) bepaalt Excel zelf automatisch. Maar je kunt ook via het eigenschappenvenster de binbreedte of het aantal bins zelf specificeren. De bijbehorende intervalgrenzen worden dan door Excel berekend. Wanneer je ook nog de grenswaarden zelf wilt bepalen, dan moet je daarvoor een aparte kolom in het werkblad opnemen.

Taak 3.6 Hulpbestand: frequenties.xlsx

  1. Open het eerder gebruikte bestand frequenties.xlsx.
  2. Selecteer een cel in het gegevensgebied op werkblad data.
  3. Kies tab Invoegen > Aanbevolen grafieken > Alle grafieken > Histogram.
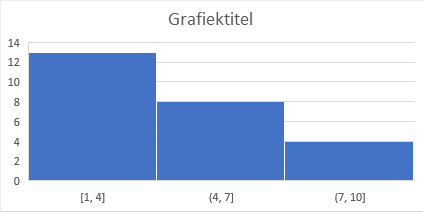
Figuur 3.12: Standaard histogram via het invoegen van een grafiek.

In Excel wordt een histogram gewoonlijk als een kolomdiagram weergegeven met labels onder het midden van de kolom. En de kolommen worden standaard aaneensluitend getekend.

Er wordt geen tabel met frequenties gegenereerd. Je kunt desgewenst de frequenties zichtbaar maken door via de grafiekopties gegevenslabels toe te voegen.

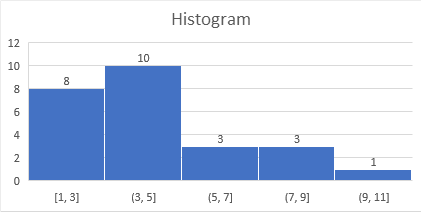
De standaard grafiek in Figuur 3.12 met drie intervallen laat te weinig details zien. In de volgende oefening wordt het aantal bins vergroot door de bin-breedte kleiner te maken.

Taak 3.7 Hulpbestand: frequenties.xlsx

  1. Selecteer horizontale as > Rechter muisklik > As opmaken.
    Maak het eigenschappenvenster breed genoeg, anders zijn niet alle invulvelden zichtbaar!

  2. Zet de bin-breedte op 2.

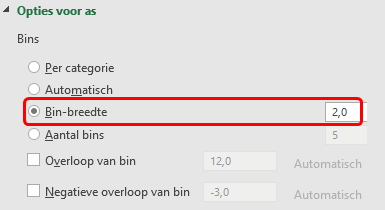
Figuur 3.13: Specificatie bins in eigenschappenvenster.
  1. Pas tevens de grafiektitel aan en voeg gegevenslabels toe. Het aangepaste histogram geeft nu wat meer informatie over de verdeling van de gegevens.
Figuur 3.14: Aangepast histogram.

3.4.2 Boxplot

Een boxplot grafiek laat zien hoe de gegevens over de kwartielen verdeeld zijn. De boxplot laat eenzelfde soort informatie zien als een histogram, maar dan met minder details. Bij een boxplot worden de gegevens verdeeld in 4 kwartielen, elk met 25% van de waarnemingen. Het centrum van de boxplot is de mediaan. In de box zitten de waarden tussen het eerste en het derde kwartiel. De lengte van de box is dus de interkwartielafstand. In Figuur 3.15 zijn de onderdelen van de boxplot getekend. De lijntjes aan de uiteinden worden ook wel snorharen (Eng. whiskers) genoemd. In Excel heet dit grafiektype Box-and-Whisker.

Figuur 3.15: Schematische weergave van een boxplot.

In een boxplot bevat de lengte van de kwartielen ook informatie. Zo is in Figuur 3.15 het 2e kwartiel smaller dan het 3e kwartiel, de gegevens in het 2e kwartiel hebben dus een kleiner gegevensbereik dan die in het 3e kwartiel.

Vaak kom je ook iets anders getekende boxplots tegen waarbij de lijntjes aan de uiteinden niet het echte minimum en maximum zijn. Ze worden dan getekend op 1,5 keer de interkwartielafstand (= Q3 - Q1) links van Q1 en rechts van Q3. De waarnemingen die daar buiten liggen worden dan als uitbijters beschouwd en als afzonderlijke punten in de boxplox weergegeven. Een aantal statistische softwarepakketten (SPSS) doet dit zo, evenals Excel. Soms wordt ook het gemiddelde in de boxplot getekend. En verder kom je boxplots zowel horizontaal als vertikaal getekend tegen.

Je kunt dit grafiektype voor 1 variabele gebruiken, maar de kracht ervan komt pas echt naar voren wanneer je meerdere groepen met elkaar wilt vergelijken.

Taak 3.8 Hulpbestand: tablets.xlsx

Bij een produktonderzoek zijn 3 groepen van elk 10 personen gevraagd om een merk tablet (A, B, C) te evalueren, elke groep één merk. De toegekende scores van elke persoon zijn te zien in Figuur 3.16.

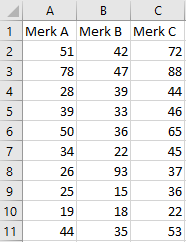
Figuur 3.16: Dataset produktonderzoek tablets.
  1. Open het bestand tablets.xlsx en selecteer het gegevensgebied A1:C11.
  2. Kies tab Invoegen > Aanbevolen grafieken > Alle grafieken > Box-and-whisker.
  3. Wijzig de titel in Beoordeling tablets en voeg een legenda aan de bovenkant toe.
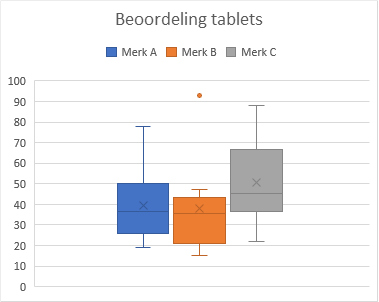
Figuur 3.17: Dataset met Boxplots voor de drie groepen.

Interpretatie

Via de boxplots kun je zien dat de scores voor merk C wat hoger lijken uit te vallen dan voor de andere twee. En die voor merk B lijken iets lager uit te vallen. De verdeling bij merk A is het meest symmetrisch, tenminste in het gebied tussen Q1 en Q3. De verdelingen bij de merken B en C zijn minder symmetrisch. Een andere beoordelingsmaatstaf voor symmetrie is hoe dicht het gemiddelde (met X aangegeven) en de de mediaan (de horizontale streep in de box) bij elkaar liggen. Merk B heeft een uitschieter naar boven (de rode punt in de figuur).

3.5 Opgaven

Oefening 3.1 In een straat wonen 9 personen met een inkomen tussen 15.000 en 30.000 euro en nog 1 persoon met een inkomen van ongeveer een miljoen. Welke maatstaf zou je gebruiken om het centrum van deze inkomens weer te geven?

Oefening 3.2 In een bedrijf met 12 werknemers zijn de verzuimdagen per werknemer in een bepaald jaar: 0, 0, 0, 2, 2, 4, 5, 6, 7, 8, 20, 30. Ga na dat gemiddelde = 7, mediaan = 4,5 en modus =0.

Oefening 3.3 Het bestand schoenmaten.xlsx bevat de schoenmaatverdeling van 3000 Nederlandse mannen. Maak een relatieve frequentieverdeling (percentages) van de schoenmaten en visualiseer het resultaat met een kolomdiagram.

Oefening 3.4 Het bestand occasions.xlsx bevat een aantal gegevens van 150 tweedehandse auto’s.

  1. Maak een kruistabel van de variabelen model en kleur.
  2. bepaal de kenmerkende statistieken voor de variabelen prijs en kmstand.

Oefening 3.5 Een steekproef van 20 leden van een golfclub naar hun lengte (in cm) heeft het volgende resultaat opgeleverd: 152, 173,175, 163,173,170, 173, 175, 196, 175, 175, 183, 175, 165, 165, 173, 163, 180,1 88, 188

  1. Maak een samenvattingsinfo van de belangrijkste statistische kenmerken via Gegevensanalyse.
  2. Maak een boxplot en een histogram en beoordeel aan de hand hiervan of de data een normale verdeling volgen.

Oefening 3.6 In het bestand studietijd.xlsx staan het aantal studie-uren die een steekproef van vrouwelijke en mannelijke studenten besteed hebben aan een bepaald vak.

  1. Bepaal de mediaan voor beide groepen.
  2. Maak een boxplot waarin de studie-uren van beide groepen met elkaar vergeleken worden.
  3. Becommentarieer de verschillen tussen de twee groepen.

Oefening 3.7 Van twee groepen van elk 50 personen is de lengte (in cm) gemeten. De resultaten zijn in het bestand groepslengtes.xlsx te vinden. Maak een boxplot voor de twee groepen en bestudeer deze. Geef aan wat je opvalt, welke verschillen er te zien zijn. Zijn er conclusies te trekken?

Oefening 3.8 In het bestand boeken.xlsx staan van een hoeveelheid boeken de volgende gegevens:

  • boekid - een unieke waarde uit het interval [1015, 9875]
  • prijs - de prijs van het boek
  • categorie - kind, roman, studie

Het onderzoek richt zich op de variabele prijs.

  1. Bepaal hiervoor de kenmerkende statistieken per categorie.
  2. Onderzoek grafisch of de variabele prijs voor de verschillende categorieën een normale verdeling volgt.