5  Tijdreeksen

Doelstellingen

• Introductie in de analyse van tijdreeksen
• Introductie van prognosetechnieken in het algemeen en de mogelijkheden met Excel
• Het opdoen van praktische vaardigheden via taken en oefeningen

5.1 Introductie

Veel bedrijfskritische beslissingen zijn afhankelijk van goede prognoses voor de toekomst. Het maken van een prognose is gebaseerd op historische gegevens en dat zijn meestal tijdreeksen, een reeks waarnemingen van een variabele gemeten op opeenvolgende tijdstippen of over opeenvolgende periodes.

De historische gegevens omvatten vaak trends, seizoenpatronen en externe factoren. Een tweetal veel voorkomende scenario’s zijn:

• Financiële prognoses voor het voorspellen van omzet, kosten en winst alsmede van indicatoren hiervoor zoals aantal nieuwe klanten of verkoopprijs.

• Vraagvoorspellingen voor producten vormen een kritische stap in de supply-chain management van een organisatie. Hierop is de inkoop van grondstoffen en inzetten van mensen en machines weer gebaseerd. Vraagvoorspelling is vaak uniek voor een bedrijfstak. Zo zal een electriciteitsbedrijf een schatting willen maken van de te leveren energie in de toekomst. En een ziekenhuis zal het aantal benodigde bedden willen plannen.

Voor een gedegen begrip van tijdreeksen en de verschillende prognosetechnieken is behoorlijke statistische kennis vereist. In dit studieboek worden de statistische achtergronden niet behandeld. Ook de hoeveelheid formules wordt zoveel mogelijk beperkt.

5.2 Wat is een tijdreeks?

Een tijdreeks is een reeks waarnemingen van een variabele gemeten op opeenvolgende tijdstippen of over opeenvolgende periodes. Wanneer de gegevens een bepaald patroon in de tijd vormen, dan kan dit patroon gebruikt worden om een prognose voor een toekomstige waarde te maken.

Het kan ook zijn dat de waarde van een variabele afhangt van andere variabelen dan de tijd. Zo zou er een verband kunnen zijn tussen de hoogte van de bloeddruk en de leeftijd. Je hebt dan een onafhankelijke variabele (leeftijd) en een afhankelijke variabele (bloeddruk). Dergelijke verbanden tussen variabelen worden onderzocht met regressie-analyse. Wanneer je de tijd als een onafhankelijke variabele beschouwt, dan kan regressie-analyse ook bij tijdreeksen worden gebruikt.

De meetgegevens van de variabele bestaan uit herhaalde metingen op vaste tijdstippen zoals elk uur, dag, week, maand, kwartaal, jaar of elke regelmatige periode. De gegevens zijn dus geordend in de tijd en de tijd tussen elke waarneming is constant.

Voorbeelden van tijdreeksen:

• ziekteverzuim per maand of jaar
• omzet per maand
• verkopen per kwartaal
• verkeersdoden per jaar
• …

Veel tijdreeksen vertonen een trend (toename of afname) en/of zijn seizoensgebonden, dat wil zeggen variaties die specifiek voor een bepaald tijdsbestek zijn. Zo zal bijvoorbeeld de verkoop van ijs in de zomer hoger zijn dan in de winter.

5.3 Componenten tijdreeks

Een tijdreeksanalyse is de analyse van gegevens die in de loop van een bepaalde periode verzameld zijn. Het is dus een onderzoek naar de samenhang tussen twee variabelen, waarvan de onafhankelijke variabele de tijd is.

Een tijdreeksanalyse begint altijd met het weergeven van de tijdreeks in een grafiek, meestal een lijngrafiek. Op de horizontale as staat altijd de tijd en op de verticale as de te onderzoeken variabele. De grafiek geeft vaak al een eerste beeld van de kenmerken van de tijdreeks.

Figuur 5.1: Tijdreeks van het aantal internationale vliegtuigpassagiers per maand (1949-1960)

Je ziet hierin onmiddellijk een paar zaken:

1. Het aantal passagiers neemt in de loop van de tijd toe.
2. Er vinden jaarlijks terugkerende patronen plaats: periodiek gedrag.
3. De variantie lijkt in de tijd toe te nemen: de uitzwaaiers worden groter.

Zaken waar je op moet letten zijn:

• Is er een trend? Dit houdt in dat de variabele de neiging heeft toe te nemen (continu stijgend) of af te nemen (continu dalend).
• Is er seizoensgebondenheid? Dit houdt in dat er een regelmatig terugkerend patroon van pieken en dalen te zien is, gerelateerd aan bepaalde tijdsdelen zoals seizoenen, kwartalen, maanden, weekdagen, enz.
• Zijn er uitschieters? Dit zijn waarden die ver verwijderd zijn van de andere waarden.
• Is er een lange termijn cyclus? Deze is niet gerelateerd aan de seizoensfactoren.
• Is er een constante variantie van de variabele over de tijd of wordt deze groter of kleiner?
• Zijn er plotselinge wijzigingen in de grootte of de variantie?

Bij een nauwkeuriger analyse van een tijdreeks is het nuttig wanneer je dergelijke zaken apart zou kunnen bekijken. Daarvoor moet je een tijdreeks in de verschillende componenten kunnen splitsen. Bij de meest gebruikte systematiek gaat men er van uit dat een tijdreeks uit de volgende componenten bestaat:

Figuur 5.2: Componenten van een tijdreeks.

Trend

Hoewel tijdreeksgegevens over het algemeen willekeurige fluctuaties vertonen, kan een tijdreeks over een langere periode ook geleidelijk stijgen of dalen. Dit patroon wordt een trend genoemd. Een trend is meestal het resultaat van langetermijnfactoren zoals bevolkingstoename of -afname, verschuivende demografische kenmerken van de bevolking, verbeterde technologie, veranderingen in het concurrentielandschap en/of veranderingen in consumentenvoorkeuren.\

In Figuur 5.3 zie je de fietsverkopen van een bepaalde fabrikant over 10 jaar. De gegevens zijn te vinden in bestand fietsen.xlsx.

Figuur 5.3: Verkoop fietsen over 10 jaar.

De grafiek vertoont enige op- en neerbeweging, maar lijkt een systematisch stijgende trend te vertonen.

Seizoen

Dit zijn regelmatige schommelingen (fluctuaties) per dag/maand/kwartaal (meestal binnen een jaar). Zo zullen ijsverkopen in de zomer hoger zijn dan in de winter. En de verkopen van sneeuwruimers zullen tegenovergesteld patroon vertonen. Seizoensgebondenheid betreft altijd een vaste en bekende periode.

In Figuur 5.4 is het seizoenspatroon van de kwartaalverkopen van paraplu’s door een winkel over vijf jaar te zien. De gegevens zijn te vinden in bestand paraplu.xlsx.

Figuur 5.4: Seizoencomponent aantal internationale vliegtuigpassagiers.

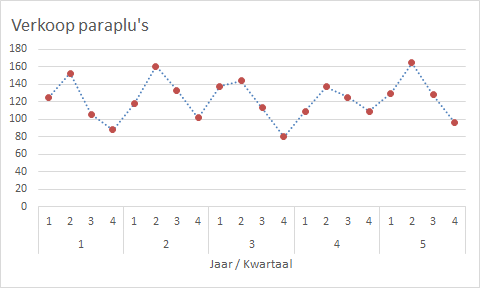
De grafiek wijst niet op een langetermijntrend in de verkoop. Oppervlakkig bekeken ziet het eruit als een horizontaal patroon met willekeurige fluctuaties. Wanneer je beter kijkt zie je een systematisch patroon. Zo heeft binnen elk jaar het 2^e kwartaal steeds de hoogste omzet en het 4^e kwartaal de laagste omzet. Er lijkt dus sprake van een kwartaalpatroon.

Random

Dit zijn onregelmatige schommelingen die niet uit een van de eerder genoemde onderdelen verklaard kunnen worden. Ze worden ook wel toevallige invloeden genoemd.

Figuur 5.5: Onregelmatige schommelingen met gemiddelde 0.

Dit is een voorbeeld van een zogenaamde stationaire tijdreeks. Dat is een tijdreeks waarvan de statistische eigenschappen onafhankelijk zijn van de tijd. Dit houdt het volgende in: Het gemiddelde en de variantie zijn constant en er is geen autocorrelatie (correlatie met voorgaande gegevens.

De grafiek van een stationaire tijdreeks zal altijd een horizontaal patroon met willekeurige fluctuaties vertonen.

Cyclisch

Dit zijn schommelingen (golfbewegingen) over een langere periode, vaak vele jaren, door schommelingen in de conjunctuur. Kenmerkend is ook dat deze periodes geen vaste periode hebben, in tegenstelling tot een seizoenspatroon. Veel economische tijdreeksen vertonen cyclisch gedrag. Het patroon heeft wel wat weg van een sinusvorm, een globale stijging wordt gevolgd door een globale daling. De duur van deze schommelingen is meestal een paar jaar.

Figuur 5.6: Voorbeeld van een cyclisch patroon.

In veel gevallen wordt de cyclische component weggelaten of gecombineerd met de trend tot één trendcyclus.

5.4 Modellen

Er worden twee wiskundige modellen voor tijdreeksen gehanteerd: Additief en Multiplicatief. En het ontleden van de tijdreeks in de afzonderlijke componenten heet decompositie van de tijdreeks.

5.4.1 Additief model

Je kiest hiervoor wanneer de seizoenseffecten in grootte nagenoeg constant blijven.

\(Y_t = T_t + S_t + R_t\)

• \(Y_t\) - de waargenomen waarde in de tijdreeks op tijdstip \(t\)
• \(T_t\) - waarde trend component op tijdstip \(t\)
• \(S_t\) - waarde seizoen component op tijdstip \(t\)
• \(R_t\) - waarde random component op tijdstip \(t\)

Je telt dus gewoon de waarden van de drie componenten op om de waarde in de tijdreeks te krijgen.

5.4.2 Multiplicatief model

Je kiest hiervoor wanneer de seizoenseffecten in grootte toenemen of afnemen.

\(Y_t = T_t \times S_t \times R_t\)

• \(Y_t\) - de waargenomen waarde in de tijdreeks op tijdstip \(t\)
• \(T_t\) - waarde trend component op tijdstip \(t\)
• \(S_t\) - seizoenindex op tijdstip \(t\)
• \(R_t\) - randomindex op tijdstip \(t\)

De trend wordt gemeten in eenheden van de variabele in de tijdreeks. De seizoenscomponenten en onregelmatige componenten worden echter relatief gemeten, waarbij waarden boven de 1,00 duiden op effecten boven de trend en waarden onder 1,00 op effecten onder de trend. Om de tijdreekswaarde te krijgen worden deze drie componenten met elkaar vermenigvuldigd. Veel zakelijke en economische tijdreeksen volgen dit patroon.

In Figuur 5.1 zie je de seizoenseffecten steeds groter worden, hier past dus een multiplicatief model bij.

Een multiplicatieve tijdreeks kan via de logaritme functie omgezet worden in een additieve tijdreeks:

\(log(T*S*C*R) = log(T) + log(S) + log(C) + log(R)\)

Er zijn verschillende methodes voor het bepalen van de afzonderlijke componenten. Het gewogen gemiddelde wordt meestal gebruikt om te corrigeren voor de seizoensinvloed. Hierna wordt de trend bepaald voor de seizoengecorrigeerde reeks. Wat er dan nog overblijft is de randomcomponent. Het uitvoeren van een decompositie valt buiten het bestek van dit studieboek.

Taak 5.1 Hulpbestand: ausbeer56-73.xlsx

Als voorbeeld van een tijdreeks wordt de bierproductie (in megaliters) in Australie voor de jaren 1956-1973 bekeken en geanalyseerd.

1. Open het hulpbestand.

2. Selecteer een cel in de tabel en kies dan tab Invoegen > Draaigrafiek (groep Grafieken) > Draaigrafiek > OK. Op een nieuw werkblad wordt een lege draaitabel aangemaakt.

3. Voeg het veld Volume toe aan het gebied Waarden en het veld Datum aan het gebied As (categorieën). Naast het veld Datum worden automatisch ook de velden Jaren en Kwartalen aangemaakt.

De naam van het eigenschapvenster en de namen van de gebieden die getoond worden hangen af van of je de grafiek of de draaitabel geselecteerd hebt.

selectie grafiek

• naam eigenschapvenster: Draaigrafiekvelden
• gebieden: Filters, Legenda (reeks), As (categorieën) en Waarden.

selectie draaitabel

• naam eigenschapvenster: Draaitabelvelden
• gebieden: Filters, Kolommen, Rijen, en Waarden.

4. Wijzig het grafiektype in Lijn met markeringen.

5. Selecteer in de draaitabel een willekeurig jaar. Daarna Rechter muisknop > Uit- en samenvouwen > Gehele veld uitbreiden.
   Zowel in de draaitabel als draaigrafiek worden de jaren uitgesplitst in kwartalen. In principe is de tijdreeks nu zichtbaar. Echter de layout kan nog verbeterd worden.

6. Breng de volgende wijzigingen in de lay-out aan:

   • Verwijder het veld Datum uit het gebied As in de lijst met Draaitabelvelden.
   • Wijzig in de draaitabel in de cel rechtsboven de tekst Som van Volume in Bierproductie. Hierdoor wijzigt ook de tekst linksboven in de draaigrafiek.
   • Schaal de Y-as van 200 tot 600 met stappen van 50.
   • Voeg een titel aan de Y-as toe.
   • Verwijder de legenda en grafiektitel.
   • Maak de lijn iets dunner en geef de markeringspunten een andere kleur dan de lijn.
   • Pas eventueel de afmetingen aan.

Het resultaat zie je in Figuur 5.7.

7. Bewaar het bestand.

Figuur 5.7: Australische bierproductie (megaliters) per kwartaal.

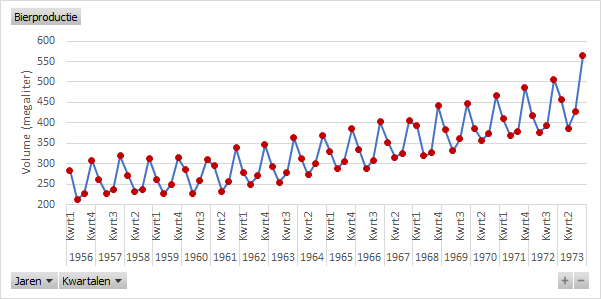
In Figuur 5.7 zie je de volgende kenmerken:

• Er is een opwaartse trend, mogelijk geen rechte lijn maar iets gebogen.
• Er is een sterke seizoensgebondenheid te zien door de regelmatige pieken en dalen gerelateerd aan de verschillende kwartalen. De top ligt steeds bij kwartaal 4, de dalen bij de kwartalen 2 en 3 en de waarden voor kwartaal 1 liggen tussen piek en dal.
• Er zijn geen uitschieters.
• Er is geen lange termijn cyclus.
• De variantie in de waarden lijkt iets toe te nemen in de tijd.

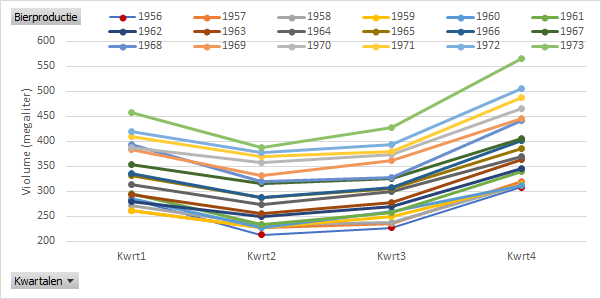
Om een beter beeld te krijgen van de seizoensgebondenheid wordt de grafiek gewijzigd zodat de gegevens voor elk jaar worden uitgezet tegen de afzonderlijke kwartalen.

Taak 5.2 Bestand: ausbeer56-73.xlsx (uit Taak 5.1)

1. Verplaats in de lijst met draaitabelvelden het veld Jaren van het gebied As naar het gebied Legenda.

2. In de draaigrafiek:

   • Voeg een legenda toe aan de bovenkant.
   • Rechter muisklik op de legenda en kies dan uit het snelmenu Legenda opmaken. Deselecteer: De legenda weergeven zonder dat deze de grafiek overlapt.
   • Rechterhuisklik op de legendaknop en kies Legendaveldknopppen verbergen in de grafiek.

In de nu ontstane grafiek Figuur 5.8 is de seizoensgebondenheid duidelijk waar te nemen.

Figuur 5.8: Jaarlijkse Australische bierproductie (megaliters) per kwartaal.

Om het gedrag per kwartaal te bestuderen worden de gegevens voor elk kwartaal uitgezet tegen de jaren.

3. Verwissel de velden Jaren en Kwartalen in de lijst met draaitabelvelden, dan staat Jaren in het gebied As en Kwartalen in het gebied Legenda.

Figuur 5.9: Jaarlijkse Australische bierproductie (megaliters) per kwartaal.

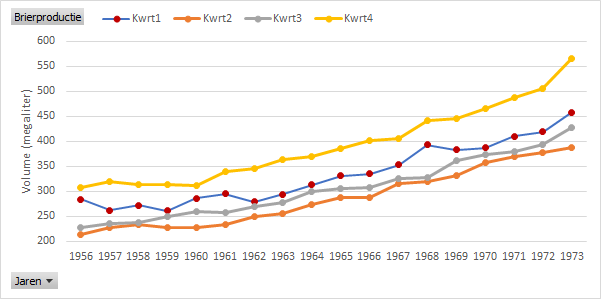
Nu kun je goed zien dat de eerder waargenomen stijgende trend voor elk kwartaal geldt.

5.5 Voortschrijdend gemiddelde

Het voortschrijdend gemiddelde, Moving Average (MA), is een gemiddelde van een vast aantal opeenvolgende waarnemingen. De verzameling waarnemingen waarover het gemiddelde berekend wordt, schuift mee in de tijd. Het aantal van deze waarnemingen wordt ook wel de vensterbreedte genoemd van een venster dat als het ware over de waarnemingen wordt gelegd. Door het venster steeds één periode op te schuiven ontstaat een reeks van gemiddelden. Deze reeks van gemiddelden geeft een gladder (smooth) verloop van de tijdreeks weer, doordat seizoensinvloeden en ruis (random component) vereffent worden, waardoor het verloop op de langere termijn (de trend) getoond wordt.

Het doel van deze vereffeningsmethode is dan ook om seizoensinvloeden en ruis te verwijderen. Daarom is de vensterbreedte meestal ook gelijk aan de lengte van het seizoen. Het voortschrijdend gemiddelde is gevoelig voor de breedte van het venster. Bij een smaller venster wordt er sneller gereageerd op veranderingen in de trend.

Er zijn twee methodes om het voortschrijdend gemiddelde te berekenen: Gecentreerd en Achterlopend.

5.5.1 Gecentreerd

Het gemiddelde wordt hier berekend voor een tijdstip \(t_n\) dat in het midden van het venster ligt. Er wordt dus het gemiddelde berekend van waarden rondom dat tijdstip. Voor een 5-punts voortschrijdend gemiddelde op tijdstip \(t_n\) bereken je dan het gemiddelde van de waarden op de tijdstippen \(t_{n-2}\), \(t_{n-1}\), \(t_n\), \(t_{n+1}\), \(t_{n+2}\). Het tijdstip \(t_n\) ligt dus in het midden van het venster. Je kunt dan geen voortschrijdend gemiddelde berekenen voor de eerste twee en de laatste twee tijdstippen in de tijdreeks.

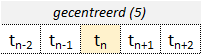
De middeling wordt dan altijd gebaseerd op een oneven aantal meetwaarden, zodat het interval symmetrisch rond \(t_n\) ligt.

Omdat bij deze methode ook altijd waarden na tijdstip \(t_n\) bekend moeten zijn, kun je deze methode niet gebruiken worden voor het maken van prognoses. De methode is wel zeer geschikt om tijdreeksen te visualiseren en seizoensinvloeden en ruis te onderdrukken.

5.5.2 Achterlopend

Hier is het tijdstip \(t_n\) waarvoor het voortschrijdend gemiddelde bepaald wordt de laatste periode in het venster. Het gemiddelde wordt dus berekend uit waarden op tijdstip \(t_n\) en daarvoor.

Voor een voortschrijdend gemiddelde van vijf maanden wordt de waarde voor de maand mei het gemiddelde van de waarden voor januari,februari, maart, april en mei. Het volgende voortschrijdend gemiddelde is dat voor de maand juni, dat het gemiddelde is van februari t/m juni. Dat gaat zo door tot je bij de laatste waarde uit de reeks bent. Voor de eerste vier maanden kun je geen voortschrijdend gemiddelde berekenen.

Omdat je met deze methode het voortschrijdend gemiddelde ook voor het laatste tijdstip kunt berekenen is deze methode geschikt voor het maken van prognoses. Voor visualisatie van de tijdreeks is deze methode wat minder geschikt omdat het voortschrijdend gemiddelde achter loopt en de trend minder zichtbaar wordt.

In de financiële wereld, vooral bij de analyse van aandelenkoersen, wordt voornamelijk met deze methode gewerkt.

Er zijn ook varianten met weegfactoren zodat je een gewogen voortschrijdend gemiddelde krijgt.

5.5.3 Excel berekeningen

In Excel kun je op drie manieren het voortschrijdend gemiddelde berekenen:

• Via de werkbladfunctie GEMIDDELDE().
• Via een trendlijn in een grafiek.
• Via Gegevensanalyse.

Via Werkbladfunctie

Bij gebruik van de werkblad functie GEMIDDELDE() kun je zelf kiezen welke van de hiervoor genoemde twee methodes je wilt gebruiken.

Taak 5.3 Hulpbestand: omzet2020.xlsx

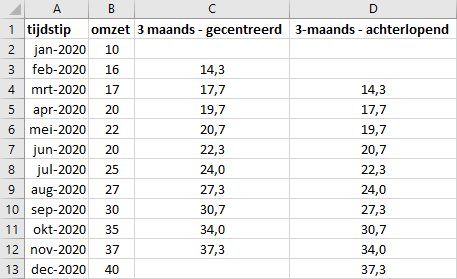
In het bestand omzet2020.xlsx staan de maandomzetten voor het jaar 2020.Het resultaat van een 3-maands voortschrijdend gemiddelde is te zien in Figuur 5.10. De werkwijze is als volgt.

1. Bepaal beide soorten voortschrijdend gemiddeldes met een vensterbreedte van 3 maanden.

   • 3 maand - gecentreerd : Typ in cel C3 de formule =GEMIDDELDE(B2:B4) en kopieer deze naar beneden t/m november.
   • 3 maand - achterlopend : Typ in cel D4 de formule =GEMIDDELDE(B2:B4) en kopieer deze naar beneden t/m december.

Figuur 5.10: Berekening 3-maands voortschrijdend gemiddelde, zowel gecentreerd als achterlopend.

3. Bewaar het bestand voor gebruik in de oefeningen hierna.

Via Trendlijn

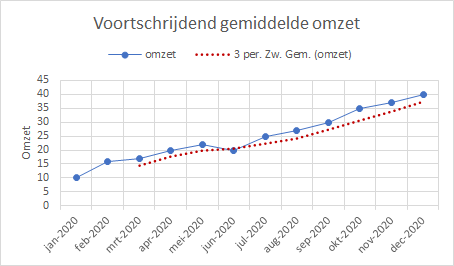
Aan een lijndiagram of spreidingsdiagram kun je de trendlijn Zwevend gemiddelde toevoegen. Deze gebruikt de achterlopende methode (middeling over voorgaande periodes) en je kunt het aantal periodes (breedte van het venster) instellen. Er wordt alleen een lijn in de grafiek geplaatst, de waarden zelf (de gemiddeldes) worden niet getoond.

Voor meer uitleg en voorbeelden over de verschillende trendlijnen in Excel zie Bijlage C.

Taak 5.4 Hulpbestand: omzet2020.xlsx

Maak een lijndiagram (met markeringen) van omzet tegen tijdstip. Voeg daarna een trendlijn Zwevend gemiddelde toe met Periode 3.

Figuur 5.11: Lijndiagram omzet-tijdstip met 3 maands voortschrijdend gemiddelde trendlijn.

Via gegevensanalyse

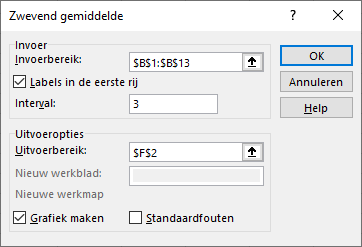
De methode via Gegevens > Gegevensanalyse > Zwevend Gemiddelde gebruikt ook het achterlopend zwevend gemiddelde.

Taak 5.5 Hulpbestand: omzet2020.xlsx

Kies Gegevens > Gegevensanalyse > Zwevend Gemiddelde.

In het dialoogscherm, zie Figuur 5.12, kun je aangeven dat je ook een grafiek wilt zien. Het aantal periodes specificeer je in het vak interval.

Figuur 5.12: Dialoogscherm Zwevend Gemiddelde.

De waarden voor de zwevend gemiddeldes worden in het werkblad geplaatst, evenals de grafiek. De uitvoer ziet er niet fraai uit en kan wel enige verbetering gebruiken. Voor een eerste indruk kan het wel voldoende zijn.

Figuur 5.13: Zwevend gemiddelde waarden en grafiek via Gegevensanalyse.

5.6 TAAK: Autoverkopen

Hulpbestand: autoverkoop.xlsx

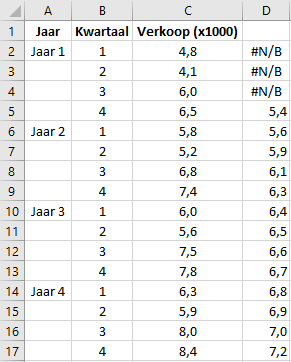
In het bestand staan de autoverkopen per kwartaal over vier jaar. De verkopen worden beïnvloed door het kwartaal. Om de trend te bestuderen wordt daarom een voortschrijdend gemiddelde gemaakt met een vensterbreedte van 4.

1. Open het bestand autoverkoop.xlsx.

2. Kies Gegevens > Gegevensanalyse > Zwevend Gemiddelde.

3. Specificeer het volgende.

   • Invoerbereik: C2:C17
   • Interval: 4
   • Uitvoerbereik: D2

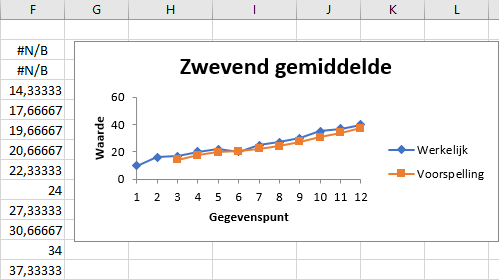
In het werkblad verschijnen de berekende gemiddeldes:

Figuur 5.14: Berekende voortschrijdend gemiddeldes.

En een lijngrafiek met de data en een voortschrijdend gemiddelde:

Figuur 5.15: Standaardgrafiek voortschrijdend gemiddeldes.

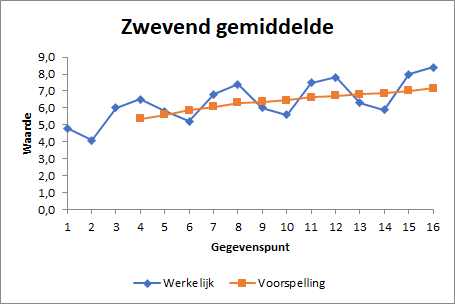
De seizoensafhankelijkheid is duidelijk zichtbaar. Het voortschrijdend gemiddelde verwijdert deze afhankelijkheid en de ruis. De overblijvende trend is nagenoeg lineair en licht stijgend.

Voor een eerste indruk is de kwaliteit van deze grafiek voldoende. Voor publicatiedoeleinden moet je de standaardgrafiek wel verbeteren, zie bijvoorbeeld Figuur 5.16.

Figuur 5.16: Aangepaste grafiek voortschrijdend gemiddeldes.

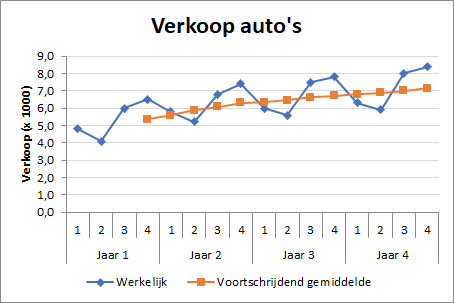
In deze grafiek zijn de volgende verbeteringen aangebracht:

• Horizontale rasterlijnen, licht gekleurd.

• Titels grafiek en Y-as.

• Labels langs de X-as en de legendatekst.

  • Selecteer de gegevensreeks in de grafiek.

  • Rechter muisklik > Gegevens selecteren > Horizontale aslabels > Bewerken en geef als Aslabelbereik op A2:B17. Daarna OK.

  • Kies Legendagegevens Voorspelling > Bewerken. Wijzig de reeksnaam in Voortschrijdend gemiddelde.

5.7 Opgaven

Oefening 5.1 Jeans verkoop

Het bestand jeans.csv bevat gegevens over de geschatte verkoop per maand van jeans, in 1000 stuks, in het Verenigd Koninkrijk gedurende zes jaren (1980 t/m 1985).

1. Download/Importeer de gegevens em maak met behulp van een draaigrafiek een diagram waarin verkoop uitgezet is tegen de tijd (jaar en maand). Ga na of er iets van een trend en/of seizoensinvloed zichtbaar is.
2. Onderzoek een mogelijk trend of seizoensinvloed nog wat beter door eerst het gedrag per jaar en daarna het gedrag per jaar via een grafiek te inspecteren.

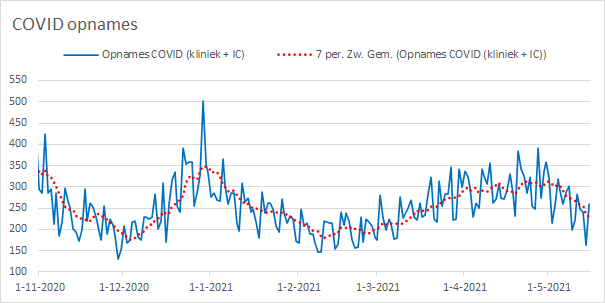
Oefening 5.2 COVID-19 opnames

Het LCPS (Landelijk Coördinatiecentrum Patiënten Spreiding) dat voor een verdeling van COVID-patiénten over de ziekenhuizen zorgt, publiceert ook een dagelijks bijgewerkte datafeed met beddenbezetting en nieuwe opnames. Voor uitleg hierover zie LCPS datafeed. Op deze site staat ook de URL om de data in csv formaat te importeren.

1. Importeer via Power Query de data (voor hulp zie Paragraaf 1.3). Geef desgewenst de kolommen aangepaste namen.
2. Maak een (lijn)diagram waarin het aantal nieuwe opnames, afzonderlijk voor kliniek en ic of bij elkaar opgeteld, wordt uitgezet tegen de datum. Laat in de grafiek de datum beginnen bij 1-11-2020.
3. Maak een 7-daags voortschrijdend gemiddelde.

Een voorbeeld van een uitwerking is te zien in Figuur 5.17. Laat je niet weerhouden om ook grafieken voor de andere variabelen te maken. Zie ook LCPS voorbeelden.

Figuur 5.17: Nieuwe COVID-19 opnames.

Oefening 5.3 Google Trends

Google houdt de populariteit van zoektermen in de loop van de tijd bij op http://www.google.com/trends . Je kunt dagelijkse gegevens bekijken door een tijdsperiode van minder dan 90 dagen te selecteren en bij een langere tijdsperiode krijg je wekelijkse of maandelijkse gegevens. De opdracht is om het volgende te vinden:

1. Een zoekterm waarin een seizoenspatroon (wekelijks of jaarlijks) herkenbaar is.
2. Een zoekterm waarin een stijgende trend herkenbaar is.

Oefening 5.4 Inkomsten uit advertenties

In het bestand advertenties.xlsx staan de inkomsten uit advertenties van een tweewekelijks verschijnend huis-aan-huisblad.

1. Maak een (lijn)grafiek waarin de inkomsten tegen het weeknummer zijn uitgezet.
2. Voeg een polynoom trendlijn toe. Experimenteer met een polynoom van de 2e, 3e en 4e graad. Verzamel voor elk van deze trendlijnen de R-kwadraat waarde. Maak een keuze voor de meest geschikte trendlijn.

Oefening 5.5 Verkoop smartphones

Het bestand smartphones.xlsx bevat de kwartaalverkopen over 4 jaar van een telefoonwinkel.

1. Maak een tijdreeksgrafiek van de verkopen.
2. Onderzoek welke componenten de tijdreeks bevat.