9 Machine Learning
Bij Machine Learning (ML), in het Nederlands ook wel statistisch leren of machinaal leren genoemd, draait alles om voorspellen. Het is een concept waarbij een programma (dit is de machine) kan “leren” van voorbeelden om patronen in gegevens te ontdekken. Je voorspelt een uitkomst op basis van een of meer kenmerken. Enkele voorbeelden.
Heeft een patiënt een bepaalde ziekte? De uitkomst van de voorspelling is het al dan niet hebben van de ziekte. En de kenmerken waar je dat op baseert zouden kunnen zijn hartslag, laboratoriumwaarden, leeftijd, geslacht, familiegeschiedenis, …
Zal een klant overstappen naar een andere energieleverancier? De uitkomst van de voorspelling is dat de klant overstapt of niet. Mogelijke kenmerken om de voorspelling op te baseren zouden kunnen zijn verbruikscijfers gas en electra, soort en duur van het contract, inkomen, betalingsachterstanden, …
Kun je de naam van een plant voorspellen op basis van een foto van die plant? De uitkomst van de voorspelling is de plantennaam of de conclusie onherkenbaar. Mogelijke kenmerken zouden kunnen zijn bladvorm, bloem, kleur, grootte, …
Je beschikt over sensorgegevens van machines (temperatuur, oliedruk, batterijconditie, stroomverbruik, …) en je wilt voorspellen welke machines in de nabije toekomst kunnen uitvallen zodat je preventief onderhoud kunt doen om deze storingen te voorkomen.
Bij de ML technieken wordt gekeken naar gelijkenis. In het voorbeeld van de energieleverancier kijk je naar andere klanten uit het verleden en selecteert degenen die qua kenmerken het meest op de huidige klant lijken. Zijn de meeste daarvan overgestapt dan is de voorspelling dat de huidige klant ook overstapt. Bedenk wel dat het een voorspelling is.
In de gegevensverzameling heb je een doelvariabele (afhankelijke variabele, uitkomstvariabele, respons) waarvan de waarde moet worden voorspeld op basis van de waarden van andere variabelen (onfhankelijke variabelen, voorspelvariabelen).
Er zijn twee soorten ML algoritmen: supervised (begeleid, gecontroleerd) en unsupervised (onbegeleid, ongecontroleerd). Bij een supervised methode heb je een trainingsdataset nodig om het algoritme te “trainen” tot je over de resultaten tevreden bent.
In de trainingsdataset weet je wat de waarde van de doelvariabele is, deze is bekend. Het ML algoritme kan uit de waarden van de onafhankelijke variabelen een waarde voor de doelvariabele berekenen. Door het instellen van de parameters van het algoritme probeer je een optimale situatie te bereiken waarbij de berekende waarden van de doelvariabele zo goed mogelijk bij de bekende waarden passen. Dit is dus het trainen. Dit trainen wordt ook wel modelleren genoemd en de optimale situatie het model.
Voor nieuwe invoergegevens waarbij dus de waarde van de doelvariabele onbekend is, kan dan door het algoritme een voorspelling gemaakt worden op basis van het model. Wanneer op een later tijdstip de echte waarde van de doelvariabele bekend is, kan de voorspelling geëvalueerd worden op nauwkeurigheid. Als de nauwkeurigheid niet acceptabel is, kun je het ML-algoritme opnieuw trainen met een steeds grotere trainingsdataset. Het algoritme leert op deze manier om steeds beter voorspellingen voor nieuwe gegevens te maken.
Bij een supervised methode wordt de totale dataset gesplitst in een groot gedeelte voor het trainen van het algoritme en een kleiner gedeelte voor het testen van het getrainde algoritme.
Bij een unsupervised methode heb je dit niet. Het model probeert patronen en relaties in de dataset te vinden door er clusters in te maken. Het model kan geen labels aan de clusters toekennen. Het kan dus niet zeggen dat zijn appels en dat zijn peren. Het model kan wel een hoop appels en peren in twee clusters verdelen, dus de appels van de peren scheiden op basis van verschillen in kenmerken. Bij een toevoegen van een nieuwe vrucht (appel of peer) kan het deze dan aan een van beide clusters toevoegen.
Het doel is om de gegevens te verkennen en er een structuur in te vinden. Deze leertechniek werkt goed op transactiegegevens. Het kan bijvoorbeeld segmenten van klanten met vergelijkbare kenmerken maken die vervolgens op dezelfde manier kunnen worden behandeld in marketingcampagnes.
Excel
Excel is niet echt geschikt om Machine Learning technieken toe te passen. Daarvoor kun je beter software als R, Python, Tableau, RapidMiner, … gebruiken. Wel kun je het principe van sommige technieken, zoals KNN, goed met behulp van Excel leren begrijpen.
Met Excel kun je transparant met gegevens werken. Bij elke stap kun je direct het resultaat zien. Je kunt tussenresultaten in de berekeningen opnemen om te zien hoe het algoritme uitgevoerd wordt, waardoor je een goed inzicht in het proces krijgt.
Voor het echte werk is Excel te beperkt en zijn de ML-methodes te complex.
9.1 KNN
Een van de eenvoudigste algoritmes is KNN, wat staat voor k-Nearest-Neighbor, oftewel de \(k\) dichstbijzijnde buren. Wanneer je het voor classificatie gebruikt, dan wordt een nieuw gegevenspunt in een doelgroep (klasse) ondergebracht op basis van de kenmerken van de \(k\) buren, de dichtstbijgelegen gegevenspunten.
De gegevens voor onderstaande voorbeelden zitten in het bestand ml-knn.xlsx zodat je zelf hiermee kunt experimenteren.
Voorbeeld met 1 kenmerk
Stel je hebt een groep van 8 personen, 4 mannen en 4 vrouwen, waarvan de lengte (cm) bekend is. Bij deze groep komt nu een nieuwe persoon waarvan je alleen de lengte weet, 176 cm. Kun je dan hiermee voorspellen of het een man of een vrouw is?
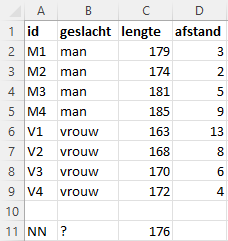
Voor een vergelijking zijn in figuur Figuur 9.2 de lengtes van alle personen op een denkbeeldige meetlat afgebeeld.

Het KNN algoritme berekent nu de afstanden van de nieuwe persoon tot alle gecategoriseerde personen, waarvan het geslacht dus bekend is. Onder afstand wordt hier dan het verschil in lengte verstaan. Deze afstanden zijn te zien in Figuur 9.1.
Vervolgens worden deze afstanden gerangschikt van de dichtstbijzijnde (meest vergelijkbare) tot de verste (de minst vergelijkbare).
De waarde voor k in het algoritme staat voor het aantal buren waarmee je gaat vergelijken. Elk van deze k buren brengt als het ware een stem uit voor de desbetreffende categorie. De conclusie of de nieuwe persoon een man of een vrouw is wordt dan getrokken op basis van de meeste stemmen.
k=1: De dichtstbijzijnde persoon is M2. Conclusie: nieuwe persoon = mank=2: De dichtstbijzijnde personen zijn M2 en M1. Conclusie: nieuwe persoon = mank=3: De dichtstbijzijnde personen zijn M2, M1 en V4. Conclusie: nieuwe persoon = man
Om de situatie te voorkomen waarbij de stemmen staken kun je voor \(k\) het beste een oneven getal nemen.
Voorbeeld met 2 kenmerken
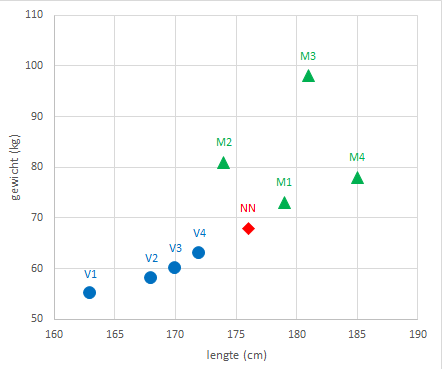
Nu is van de 4 mannen en 4 vrouwen naast de lengte (cm) ook het gewicht (kg) bekend. En het gewicht van de nieuwe persoon is 68 kg.
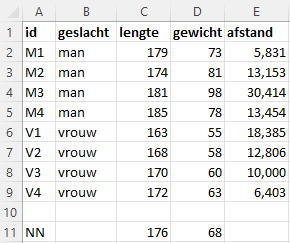
In Figuur 9.4 is een spreidingsdiagram van gewicht tegen lengte te zien.
Ook nu wordt weer de afstand bepaald van de nieuwe persoon tot de andere personen. Bij twee variabelen wordt de Euclidische afstand bepaald. Voor twee punten \((x_1,y_1)\) en \((x_2,y_2)\) kun je deze via Pythagoras uitrekenen:
\[\text{afstand } = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}\]
In Figuur 9.3 is de berekende afstand te zien. Daarna wordt weer gekeken welke de dichtstbijzijnde buren zijn.
k=1: De dichtstbijzijnde persoon is M1. Conclusie: nieuwe persoon = mank=2: De dichtstbijzijnde personen zijn M1 en V4. Conclusie: geen uitsluitsel, stemmen stakenk=3: De dichtstbijzijnde personen zijn M1, V4 en V3. Conclusie: nieuwe persoon = vrouw
Voorbeeld met 2 gestandaardiseerde kenmerken
Verschillende variabelen hebben verschillende schaaleenheden, zoals hier de lengte in cm en het gewicht in kg. Dat kan er voor zorgen dat variabelen die op een grotere schaal gemeten worden een groter aandeel hebben in de berekende afstand en daardoor belangrijker worden gemaakt dan variabelen die op een kleinere schaal gemeten worden. Om dit te voorkomen kun je de gegevens transformeren naar een nieuwe schaal. Een veel gebruikte techniek hiervoor is de min-max normalisatie waarbij de gegevens geschaald worden naar het bereik [0,1]. Hiervoor wordt de kleinste en de grootste waarde van de gegevens bepaald. Vervolgens worden de gegevens gewijzigd via
\(\text{genormaliseerde waarde } = \frac{x - min(x)}{max(x) - min(x)}\)
In Figuur 9.5 zijn de variabelen lengte en gewicht genormaliseerd en is de afstand voor de genormaliseerde gegevens berekend. En in Figuur 9.6 zie je de bijpassende grafiek.
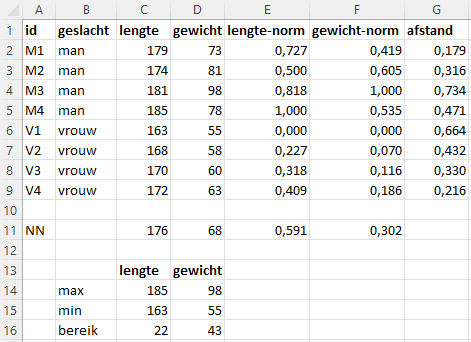
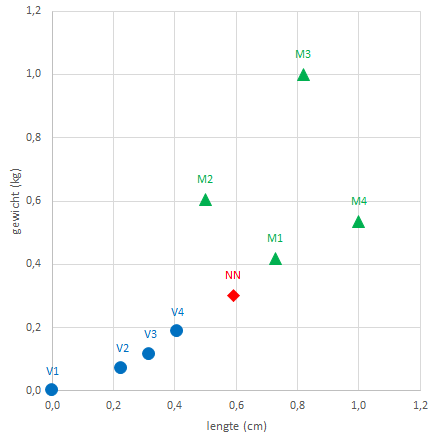
Wanneer nu naar de dichtstbijzijnde buren gekeken wordt zijn de resultaten iets anders.
k=1: De dichtstbijzijnde persoon is M1. Conclusie: nieuwe persoon = mank=2: De dichtstbijzijnde personen zijn M1 en V4. Conclusie: geen uitsluitsel, stemmen stakenk=3: De dichtstbijzijnde personen zijn M1, V4 en M2. Conclusie: nieuwe persoon = man
Meer dan 2 kenmerken
Voor meer attributen, bijvoorbeeld door de gegevens aan te vullen met de taillemaat, is het principe hetzelfde. Je kunt het wat moeilijker tekenen en ook het berekenen van de afstand is wat meer werk.
\[\text{afstand} = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2 + (z_1 - z_2)^2 + ... }\]
kNN in de praktijk
In de praktijk heb je met grotere datasets te maken. Om de beste waarde voor \(k\) te vinden wordt dan de dataset gesplitst in een groter deel van zo’n 70%-80% van de gegevens om het model te trainen en een resterend kleiner deel om het model te testen. Het trainen en testen gebeurt voor verschillende waarden van \(k\). Die waarde van \(k\) welke de kleinste voorspelfout geeft wordt dan als beste waarde voor het model gebruikt.
9.2 K-Means clustering
K-Means is een unsupervised ML methode om clusters van waarnemingen in een dataset te ontdekken. Er zijn meerdere methodes om te clusteren, maar k-means is een van de oudste en meest toegankelijke.
Het doel van clustering is om de waarnemingen groeperen in clusters die vergelijkbare kenmerken hebben. De waarnemingen binnen een cluster lijken meer op elkaar dan op waarnemingen in andere clusters.
Clustering wordt door bedrijven gebruikt voor het segmenteren van klanten in groepen met een vergelijkbare aankoopgeschiedenis, die dan gebruikt kunnen worden voor gerichte advertentiecampagnes.
Bij k-means is k het aantal clusters en wordt elke cluster gekenmerkt door een centrum (zwaartepunt). Een waarneming wordt ondergebracht in de dichtsbijzijnde cluster, dat is de cluster met de kortste afstand naar het centrum ervan.
Er bestaan verschillende manieren om de afstand te bepalen. De meest gebruikte is de Euclidische afstand (bekend van de stelling van Pythagoras).
Heb je twee punten met de coördinaten \((x_1, x_2)\) en \((y_1, y_2)\) dan is de Euclidische afstand uit te rekenen via de bekende Stelling van Pythagoras.
\[\text{afstand = } \sqrt{(x_1 - y_1)^2 + (x_2 - y_2)^2}\]
Zijn er meer variabelen voor elke waarneming, bijvoorbeeld \((x_1, x_2, x_3, x_4)\) en \((y_1, y_2, y_3, y_4)\) dan wordt de afstand op analoge wijze bepaald. Bijvoorbeeld voor vier variabelen:
\[\text{afstand = } \sqrt{(x_1 - y_1)^2 + (x_2 - y_2)^2 + (x_3 - y_3)^2 + (x_4 - y_4)^2}\]
Het algoritme werkt als volgt.
Begonnen wordt met het willekeurig kiezen van het centrum voor elke cluster.
Daarna wordt voor elke waarneming de afstand tot het centrum van elke cluster bepaald.
Elke waarneming wordt nu ingedeeld bij het cluster met de kortste afstand tot het centrum.
Voor elke cluster wordt een nieuw centrum bepaald op basis van de gemiddelde waarden van alle waarnemingen binnen dat cluster.
De stappen 2 t/m 5 worden herhaald tot de positie van de clustercentra niet meer wijzigt.
Voorbeeld
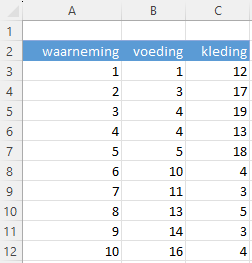
Het gegevensbestand ml-kmeans.xlsx bevat een werkblad data met 10 waarnemingen van de gemiddelde uitgaven voor voeding en kleding (zie Figuur 9.7).
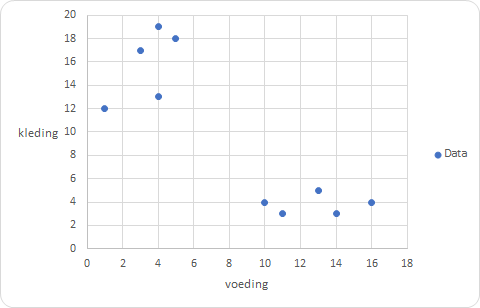
Wanneer je de waarnemingen uitzet in een spreidingsdiagram, zie Figuur 9.8, dan kun je visueel de waarnemingen al in 2 clusters indelen, een groep linksboven en een groep rechtsonder. Eventueel kun je de groep linksboven nog verder opsplitsen in twee groepen zodat het totaal aantal clusters dan 3 wordt.
Voor de implementatie van k-means wordt een model met 3 clusters opgezet. Aan het eind wordt nog bekeken of een model met 2 clusters een betere optie is.
Model met 3 clusters
Om de oorspronkelijke dataset intact te houden wordt een kopie van het werkblad data gemaakt en hernoemd als model3.
In Figuur 9.9 zie je het gemaakte k-means model.
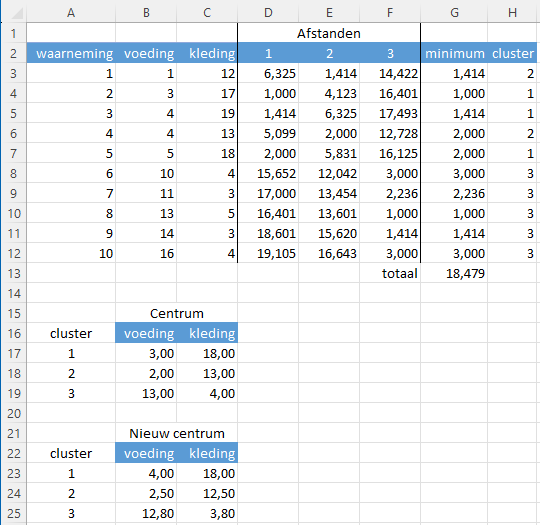
In de cellen B17:C19 zie je de willekeurig gekozen waarden voor het centrum van de drie clusters.
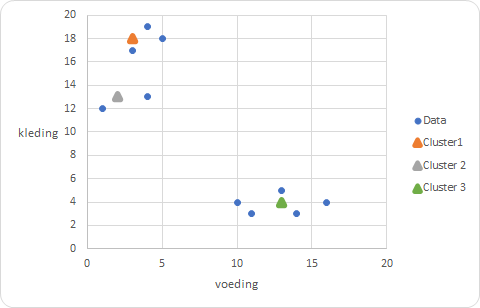
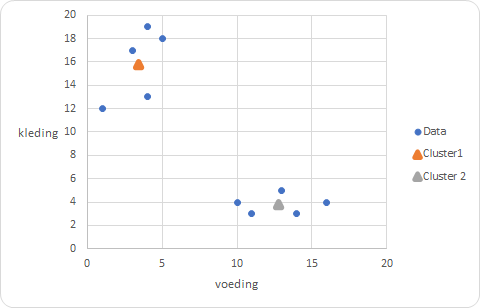
Om inzichtelijk te maken waar elk centrum ligt ten opzichte van de waarnemingen zijn deze ook aan het spreidingsdiagram toegevoegd, zie Figuur 9.10. Wanneer je naar het spreidingsdiagram kijkt, dan zijn er betere waarden voor de clustercentra mogelijk.
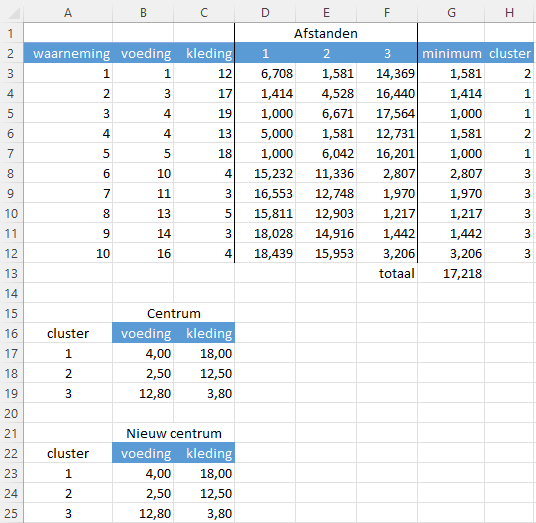
De kolom met de naam 1 bevat de afstand van elke waarneming tot het centrum van cluster 1, kolom 2 de afstand tot het centrum van cluster 2 en kolom 3 de afstand tot het centrum van cluster 3.
De formule in cel D3 is =WORTEL(($B3-$B$17)^2+($C3-$C$17)^2). Deze kun je daarna naar rechts en naar beneden kopieren zodat het bereik D3:F12 met de berekende afstanden gevuld wordt.
De kolom met de naam minumum bevat de kortste afstand van de waarneming naar een van de drie centra. De formule in cel G3 is =MIN(D3:F3) en deze kun je weer naar beneden kopieren tot G12. In cel G13 wordt het totaal van deze kortste afstanden berekend.
In de kolom met de naam cluster wordt vervolgens vastgesteld in welke cluster de waarneming moet vallen. In cel H3 staat hiervoor de formule =VERGELIJKEN(G3;D3:F3;0) welke je weer naar beneden kunt kopieren.
Nu voor elke cluster bekend is welke waarnemingen tot de cluster behoren, kan voor elke cluster een nieuwe waarde voor het centrum berekend worden. Hiervoor worden de gemiddeldes van voeding en kleding berekend voor de waarnemingen binnen elke cluster. Dat is gebeurd in de cellen B23:C25. Zo is de formule in cel B23 =GEMIDDELDE.ALS($H$3:$H$12;$A23;B$3:B$12). Ook deze kun je weer kopieren zodat het bereik B23:C25 de juiste formules bevat.
Nu kan het iteratieproces beginnen. Kopieer de nieuwe centrumwaarden naar B17:C19.
Let er op dat je de waarden kopieert via Plakken Speciaal > Waarden plakken en dat niet de formules gekopieerd worden.
Er worden nu weer nieuwe centrumwaarden berekend en ook neemt de som van de minimum afstanden af. In de grafiek kun je ook zien dat de drie centra verschuiven in de richting van de cluster.
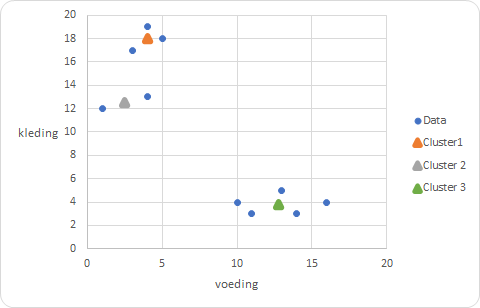
Herhaal dit proces totdat er nauwelijks meer wijzigingen optreden. Dat is bij dit voorbeeld al snel het geval. In Figuur 9.11 zie je de gevonden waarden voor de drie centra en de clusterindeling voor de waarnemingen.
En in Figuur 9.12 kun je de lokaties van de clusters waarnemen die waarschijnlijk wel overeenkomen met de eerste gedachte.
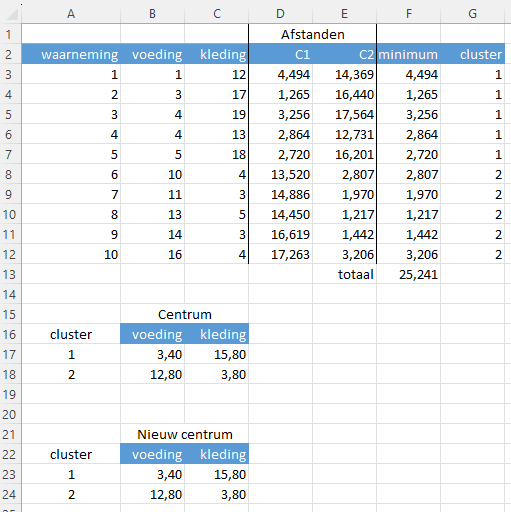
Model met 2 clusters (k=2)
Het handigste om een model met 2 clusters te maken is door te beginnen met het maken van een kopie van werkblad model3 en deze te hernoemen naar model2. Vervolgens verwijder je de kolom D3 en de rijen voor cluster 3.
Start met willekeurig gekozen beginwaarden voor de clustercentra. De eindresultaten zijn te zien in Figuur 9.13 en Figuur 9.14.
De beste waarde voor k
Om de beste waarde voor k te vinden wordt naar de som van de minimale afstanden gekeken, welke je zo klein mogelijk wilt hebben. Bij dit voorbeeld is dat het geval voor k=3.
| k | som minimale afstanden |
|---|---|
| 2 | 25,241 |
| 3 | 17,218 |
In deze uitwerking heb je de iteraties handmatig uitgevoerd door steeds betere centrumwaarden te bepalen en deze weer in het model te gebruiken. In plaats daarvan zou je ook gebruik kunnen maken van de Oplosser, een met Excel meegeleverde invoegtoepassing. In dat geval is de te minimaliseren doelfunctie de cel met de som van de minimale afstanden en zijn de centrumwaarden de variabele cellen.