7 Exploratieve Data Analyse

Doelstellingen

Exploratieve Data Analyse (EDA) is vaak de eerste stap naar het visualiseren en transformeren van de gegevens. Je leert de gegevens kennen, vaak resulterend in een eerste aanzet tot modelvorming.

7.1 Introductie

Van EDA wordt wel eens gezegd dat het een zich herhalende cyclus is van

het genereren van vragen over de data.
het zoeken naar antwoorden door de gegevens te visualiseren, transformeren en modelleren.
uit het geleerde de vragen te verfijnen of nieuwe vragen te genereren.

Het doorlopen van deze cyclus is geen formeel proces met strakke regels. Zie het meer als een creatief proces om elk opkomend idee te onderzoeken. Sommige ideeën zullen op een dood spoor eindigen, andere zullen tot een vervolg leiden.

Bij EDA gaat het om

Het verkrijgen van zoveel mogelijk inzicht in de dataset.
Het herkennen van de belangrijkste variabelen.
Het herkennen van eventuele uitschieters, onregelmatigheden en fouten.
Het herkennen van patronen in de data, zoals trends, seizoensinvloeden, groeperingen (clusters) en afwijkingen hierop.
Het onderzoeken naar een mogelijk verband tussen variabelen.
Het testen van aannames die zijn gedaan over het voorspellende en/of verklarende vermogen van de data.
Het spaarzaam ontwikkelen van modellen en het testen van onderliggende aannames hierbij.

Bij een goed gedocumenteerde dataset hoort ook een codeboek (data dictionary) dat kenmerken van de dataset beschrijft, zoals de betekenis en de meetniveaus van de variabelen. Wanneer dit document niet aanwezig is, zul je de betekenis van de variabelen uit hun naam moeten afleiden.

Een eerste stap is meestal de beschrijvende statistiek, waarbij je de belangrijkste statistische kenmerken van de variabelen vastlegt. Daarna stap je al snel over op visualisaties en grafieken. Deze zijn meestal gemakkelijker te interpreteren en vereisen geen geavanceerde statistische kennis. Door de gegevens te visualiseren worden verwachte of juist onverwachte eigenschappen intuïtief zichtbaar.

Voor het verkrijgen van inzicht in een gegevensverzameling kun je niet alleen afgaan op een aantal statistieken, maar moet je ook altijd grafieken maken om ideeën te onderzoeken. Tijdens verkenningen in de beginfase zijn deze grafieken (nog) niet voor publicatie bedoeld, waardoor je aan de opmaak nauwelijks aandacht hoeft te besteden. Het gaat er in eerste instantie om dat je de data leert begrijpen. Wanneer een grafiek in een latere rapportage wordt opgenomen is de opmaak natuurlijk wel van belang, dan moeten anderen jouw grafiek kunnen interpreteren.

Anscombe dataset

Dat je niet alleen maar af kunt gaan op een aantal statistieken, maar ook altijd een grafiek moet bekijken, wordt fraai gedemonstreerd met de dataset van Anscombe.

Deze klassieke dataset bestaat uit vier eenvoudige gekunstelde verzamelingen van 11 paren x- en y-waarden. Hierbij zijn de gemiddelden en de variantie van respectievelijk de vier x en y variabelen gelijk en zijn ook de onderlinge correlaties voor de vier paren x en y variabelen gelijk zijn.

In Figuur 7.1 is te zien dat de spreidingsdiagrammen voor de vier verschillende paren x en y variabelen compleet verschillend zijn.

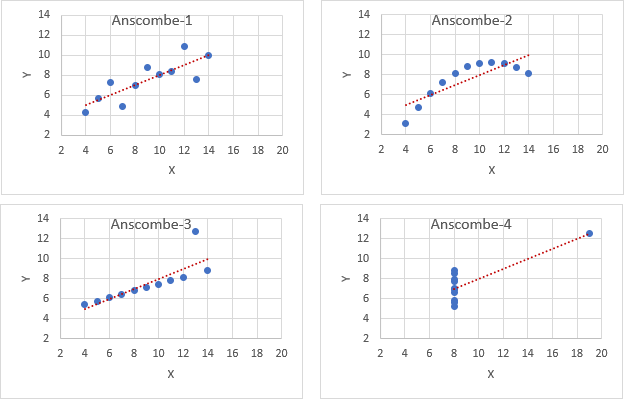
Figuur 7.1: Spreidingsdiagrammen voor de vier datasets van Anscombe.

Conclusies uit de spreidingsdiagrammen:

Anscombe-1 is duidelijk lineair met enige spreiding.
Anscombe-2 is duidelijk kwadratisch, heeft iets van een bergparabool.
Anscombe-3 heeft een duidelijke uitschieter.
Anscombe-4 heeft één enkel punt ver verwijderd van de rest van de data die dicht bij elkaar ligt.

Wanneer je zelf hiermee wilt experimenteren dan kun je het bestand anscombe.xlsx gebruiken.

7.1.1 Vragen formuleren

De beste manier om de dataset te leren begrijpen is door vragen op te stellen. Door het formuleren van een vraag wordt jouw aandacht gevestigd op een specifiek gedeelte van de dataset. Dit helpt je om te beslissen welke grafieken of samenvattingen je moet maken en of daarvoor bewerkingen van de dataset nodig zijn.

In het begin van het onderzoek is het lastig om kwalitatief goede vragen op te stellen, je kent immers de dataset nog niet. Stel daarom veel vragen op. Je hebt dan de meeste kans dat je wat interessants vindt, wat tot nieuwere of scherper geformuleerde vragen leidt.

Een aantal handige vragen die je bijna altijd kunt gebruiken zijn:

Welke variabelen heeft de dataset? Zijn ze kwantitatief (discreet / continu) of categoriaal? wat is de schaling? Welke waarden kunnen deze variabelen aannemen?
Welke variatie komt er voor in de variabelen? Dus hoe gedragen zich de waarden van een variabele.
Welke covariatie komt er voor tussen variabelen? Dus hoe gedragen zich de waarden tussen variabelen.
Is er een verband te ontdekken tussen variabelen?

7.1.2 Hulpmiddelen

Op welke manier je data kunt samenvatten en welke grafiek het meest geschikt is voor visualisatie hangt vooral van de soort variabele(n) en de vraag af. Het volgende schema kan je hierbij een handje helpen.

Figuur 7.2: Schema voor selectie samenvatting en visualisatie. In plaats van een kolomdiagram (verticaal) kun je ook een staafdiagram (horizontaal) nemen.

7.2 Eén categoriale variabele

Frequentietabellen: Je kunt absolute of relatieve frequenties gebruiken. Deze laatste wordt iets meer gebruikt omdat je hiermee kunt vergelijken hoe vaak waarden voorkomen in verhouding tot het totale aantal.
Cirkeldiagrammen: Deze vertegenwoordigen relatieve frequenties doordat ze aangeven welk deel van de gehele cirkel bij een categorie hoort. Een cirkeldiagram wordt moeilijk leesbaar wanneer je veel categorieën hebt.
Kolomdiagrammen: Hiermee kun je zowel absolute als relatieve frequenties weergeven. Bij een groot aantal categorieën kun je beter het horizontale staafdigram gebruiken.

Taak 7.1 Hulpbestand: rokers.xlsx

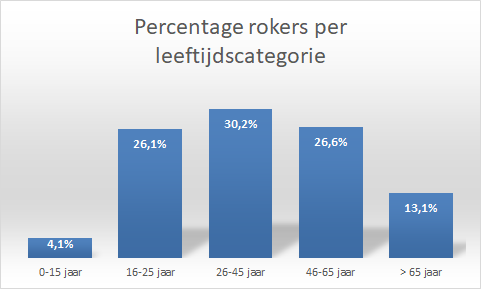
Bij een onderzoek naar rookgedrag is ook de leeftijd van de rokers verzameld. Een onderzoeksvraag is of het percentage rokers sterk verschilt per leeftijdscategorie. De leeftijdscategorieën waarin de onderzoeker in eerste instantie geïnteresseerd is zijn: t/m 15 jaar, 16-25 jaar, 25-45 jaar, 46-65 jaar, ouder dan 65 jaar.

Er moet dus een nieuwe variabele leeftijdsgroep komen met 5 categoriën en je moet dan de aantallen van leeftijd in elke categorie tellen. Omdat de klassebreedte niet overal hetzelfde is kun je geen frequentieverdeling met een draaitabel maken. Bij het werken met de functie INTERVAL() kun je zelf de grenzen van de intervallen bepalen, waardoor voor deze methode gekozen wordt.

Open het bestand rokers.xlsx en zet de kolom met leeftijden om naar een Excel tabel en geef deze een zinvolle tabelnaam, bijvoorbeeld Leeftijden, waardoor je deze naam in de formules kunt gebruiken.
Maak de volgende kolommen
- bins met de intervalgrenzen (15, 25, 45, 65).
- leeftijdsgroep met de namen van de categorieën.
- aantal voor de aantallen.
- percentage voor de percentages

De inrichting van het werkblad zou er dan als uit kunnen zien als in Figuur 7.3.

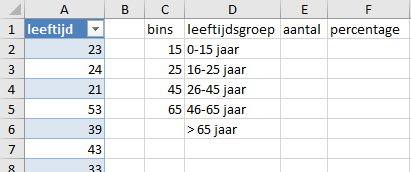
Selecteer cel E2 en voer hier in de formule =INTERVAL(leeftijden;C2:C5). Dit is een dynamische matixformule en de resultaten verschijnen in het overloopgebied E2:E6.

Voor de berekening van de percentages moet er in cel F2 een verwijzing naar het overloopgebied gemaakt worden. Dat doe je door het hash symbool # achter het adres van de eerste cel te plaatsen.

In plaats van het intypen van het adres van het overloopgebied kun je bij het invoeren van de formule ook het overloopgebied selecteren. Excel plaatst dan automatisch het juiste adres.

Plaats in cel F2 de formule =E2#/SOM(E2#). Het resultaat is te zien in Figuur 7.4.

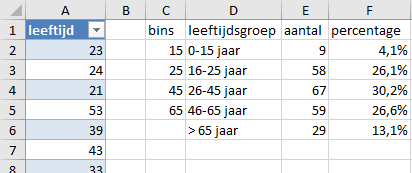
Figuur 7.4: Absolute en relatieve frequenties, berekend met de formule INTERVAL.

Maak nu een cirkeldiagram en een kolomdiagram voor een visualisatie van de frequentieverdeling. In Figuur 7.5 zie je een voorbeeld.

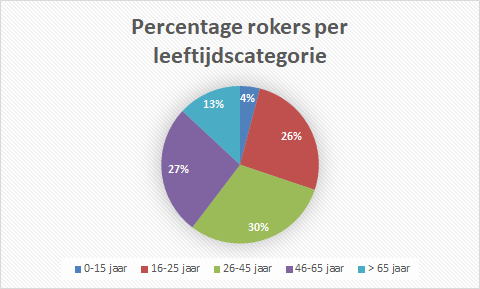
7.3 Twee categoriale variabelen

Bij twee categoriale variabelen gaat het om de verdeling van de ene variabele over de niveaus van de andere variabele.

Kruistabellen: Deze bevatten de frequenties voor elke combinatie van waarden over twee categorische variabelen.
Gegroepeerde staafdiagrammen: Een van de twee categorische variabelen wordt als groep behandeld. Binnen elke groep worden staven voor de andere categorische variabele gemaakt.

Taak 7.2 Hulpbestand: haarkleur.xlsx

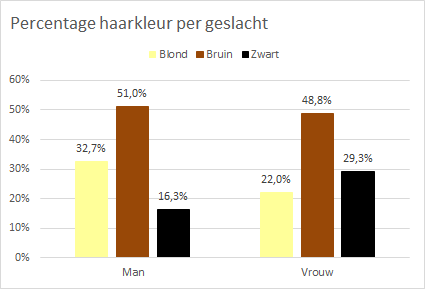
Van een groep van 90 mannen en vrouwen is de haarkleur genoteerd. Een onderzoeksvraag is of de verdeling van de kleuren sterk verschilt tussen mannen en vrouwen.

Je moet dan voor elke kleur tellen hoe vaak deze bij mannen en bij vrouwen voorkomt. Hiervoor moet je een kruistabel maken en voor een visualisatie van de verdeling leent zich een gegroepeerd kolomdiagram het beste. In Excel kun je daarvoor het handigste een draaigrafiek met draaitabel gebruiken.

Open het bestand haarkleur.xlsx en zet de kolom met gegevens om naar een Excel tabel en geef deze een zinvolle tabelnaam, bijvoorbeeld Haarkleuren.
Selecteer een cel in de tabel en kies Invoegen > Draaigrafiek > Draaigrafiek en draaitabel. Neem een nieuw werkblad als locatie voor de uitvoer en maak de volgende indeling voor de draaitabel.
- geslacht in Rijen
- haarkleur in Kolommen
- id in Waarden
Wijzig via Waardeveldinstellingen
- Aantal in plaats van Som.
- Weergave in % van rijtotaal. Hierdoor kun je de verdeling van de kleuren per geslacht bestuderen.
Pas indien wenselijk aan: titel, datalabels, kleuren, verbergen veldknoppen. Ook is de weergave van de kolomtotalen in de draaitabel niet zinvol en kun je beter niet weergeven. Een mogelijk resultaat is in Figuur 7.6 te zien.

7.4 Eén kwantitatieve variabele

Statistieken: Zoals gemiddelde, mediaan, standaarddeviatie, interkwartielafstand, 5-getallensamenvatting, … (zie Hoofdstuk 3).
Histogram: Voor een visualisatie van de verdeling van de variabele en de vorm van de verdeling.
Boxplot: Voor een visualisatie van de 5-getallensamenvatting.

Taak 7.3 Hulpbestand: maandinkomen.xlsx

Bij een steekproef van 715 personen is o.a. het netto maandinkomen verzameld. Je wilt een eerste indruk krijgen van de verdeling van de inkomens.

Open het bestand maandinkomens.xlsx en zet de kolom met gegevens om naar een Excel tabel en geef deze een zinvolle tabelnaam, bijvoorbeeld Maandinkomens.
Selecteer een cel in de tabel en kies Gegevens > Gegevensanalyse > Beschrijvende statistiek.
Specificeer het invoerbereik en selecteer bij Uitvoeropties dat er een samenvattingsinfo op een nieuw werkblad gemaakt moet worden.

De berekende getallen bevatten veel decimalen die hier weinig betekenis hebben en alleen maar zorgen voor een chaotisch beeld. Een overzichtelijker opmaak is te zien in Figuur 7.7.

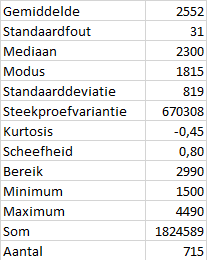
Figuur 7.7: Statistieken van de maandinkomens.

Selecteer een cel in de tabel en kies Invoegen > Aanbevolen grafieken > Alle grafieken > Box-and-whisker. Pas deze wat aan. Laat in ieder geval de gegevenslabels weergeven. Een voorbeeld is te zien in Figuur 7.8.

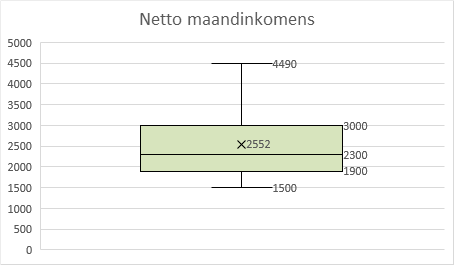
Figuur 7.8: Boxplot van de maandinkomens.

Selecteer een cel in de tabel en kies Invoegen > Aanbevolen grafieken > Alle grafieken > Histogram.

Het histogram is op zich in orde en geeft ook wel een goede indruk van de verdeling. Echter de automatisch gegenereerde bins hebben weinig zinvolle grenzen. Experimenteer daarom eens met een bin-breedte van 250 en 500.

Dat kan via Selecteer horizontale as > As opmaken > Opties voor as > Bin-breedte.

Twee voorbeelden zijn te zien in Figuur 7.9.

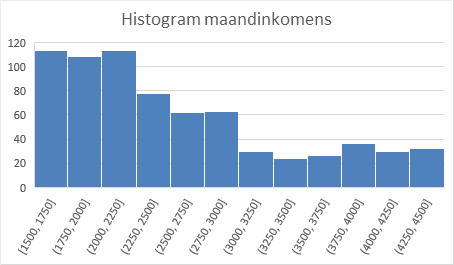
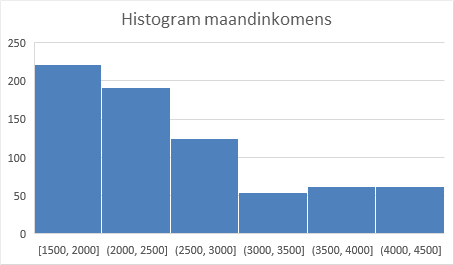
Uit de statistieken, boxplot en histogrammen krijg je een behoorlijke indruk van de verdeling.

7.5 Kwantitatieve en categoriale variabele

Boxplot (gegroepeerd): Voor het vergelijken van een variabele tusssen verschillende groepen.

Taak 7.4 Hulpbestand: lampen.xlsx

Bij een vergelijkend onderzoek van een lamptype van twee verschillende merken is ook de levensduur van de lamp getest. De onderzoeksvraag is of er een substantieel verschil in levensduur is tussen de twee merken.

Open het bestand lampen.xlsx en zet de kolom met gegevens om naar een Excel tabel en geef deze een zinvolle tabelnaam, bijvoorbeeld Lampen.
Selecteer een cel in de tabel en kies Invoegen > Aanbevolen grafieken > Alle grafieken > Box-and-whisker. Pas deze wat aan. Laat in ieder geval de gegevenslabels weergeven. Een voorbeeld is te zien in Figuur 7.10.

Figuur 7.10: Boxplot voor vergelijking levensduur lamptype van 2 merken.

7.6 Twee kwantitatieve variabelen

Spreidingsdiagram: Voor het onderzoeken van een verband tussen twee kwantitatieve variabelen.
Lijndiagram: Gebruik je voornamelijk wanneer een van de kwantitatieve variabelen een tijd weergeeft.

Bij het vergelijken van twee kwantitatieve variabelen is er meestal eerst al naar elke variabele afzonderlijk gekeken (zie Paragraaf 7.4). Bij de onderlinge vergelijking gaat het om te onderzoeken of er een mogelijk verband tussen de twee variabelen bestaat.

Bij het onderzoek naar de relatie tussen twee kwantitatieve variabelen worden de variabelen in een grafiek tegen elkaar uitgezet. Hierna kan eventueel een vervolgonderzoek komen naar de aard van de relatie. In Hoofdstuk 4 wordt op dit laatste verder ingegaan.

Taak 7.5 Hulpbestand: ijsverkoop.xlsx

Een ijsverkoper heeft gedurende 14 opeenvolgende dagen de dagtemperatuur en de dagelijkse verkoop aan ijs bijgehouden. De gegevens zijn te zien in Figuur 7.11 en staan in het bestand ijsverkoop.xlsx.

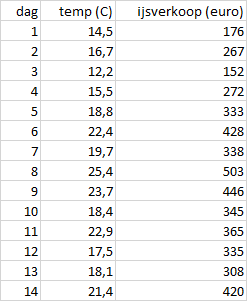
Figuur 7.11: Temperatuur (gemeten om 13:00 uur) en ijsverkoop gedurende 14 dagen.

Onderzoeksvragen: Hoe ziet het temperatuurverloop eruit en is er een verband tussen de ijsverkoop en de dagtemperatuur?

Maak een lijndiagram met de variabele dag op de X-as en de variabele temperatuur op de Y-as.
Maak een spreidingsdiagram met de variabele temperatuur als onafhankelijke variabele op de X-as en de afhankelijke variabele ijsverkoop op de Y-as.

Een voorbeeld van de resultaten is te zien in Figuur 7.12.

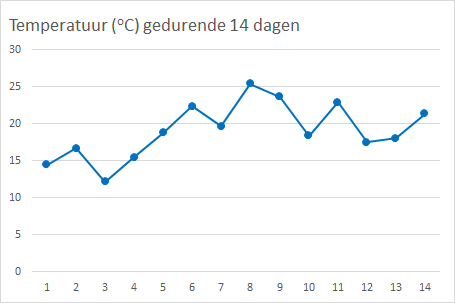
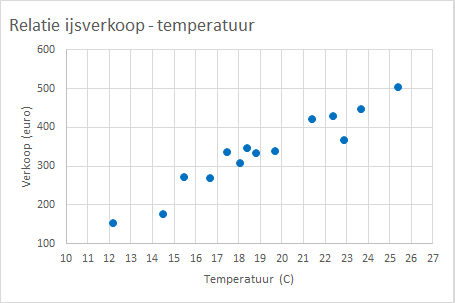
Het spreidingsdiagram toont een duidelijk positief verband te zien. Voldoende reden voor een vervolgvraag of dit een lineair verband is en zoja hoe een regressiemodel eruit zou kunnen zien.

7.7 TAAK: Old Faithful geiser

Figuur 7.13: Old Faithful geiser (bron: Detroit Free Press).

De Old Faithful geiser in Yellowstone National Park (Wyoming, VS) heeft meerdere erupties per dag. De dataset faithful.csv bevat 272 waarnemingen van twee variabelen:

eruptietijd (tijdsduur van de uitbarsting in sec.)
wachttijd (wachttijd tussen twee erupties in min.).

Aan de hand van een aantal verkenningen probeer je inzicht te krijgen in de data.

Importeer de dataset via Power Query in een Excel werkblad en sla het op onder de naam faithful.xlsx.

De variabelen eruptietijd en wachttijd worden eerst afzonderlijk bekeken, daarna gecombineerd.

7.7.1 Eruptietijd

Statistieken

Maak een samenvattingsinfo voor de variabele eruptietijd in een nieuw werkblad.

Via Gegevens > Gegevensanalyse > Beschrijvende statistiek, laat de uitvoer in een nieuw werkblad plaatsen en rond een aantal getallen af.

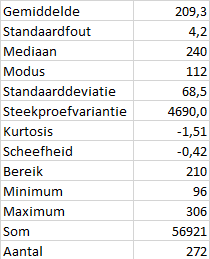
Figuur 7.14: Samenvattende statistieken eruptietijd.

Boxplot

Maak een boxplot voor eruptietijd.

Via Invoegen > Aanbevolen grafieken > Alle grafieken > Box-and-whisker

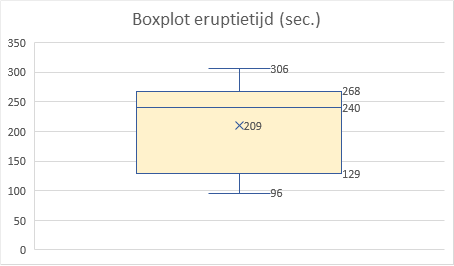
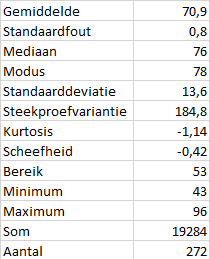
In de boxplot kun je goed zien dat de data asymmetrisch is. De mediaan (240) ligt niet in het midden van de box, maar is groter dan het gemiddelde (209). Ook ligt de mediaan veel dichter bij de maximumwaarde (306) dan bij de minimumwaarde (96). De verdeling is links scheef.

Geologische experts geloven dat er twee soorten uitbarstingen voorkomen: met een kortere en met een langere tijdsduur, die beiden een standaardlengte hebben. Rond deze waarden zou je een hogere concentratie van waargenomen lengtes verwachten. Voor het bekijken van de verdeling van de waarden van variabele eruptietijd maak je een histogram met een geschikte Bin-breedte. Om met de Bin-breedte te kunnen experimenteren moet je in Excel een histogram maken via het invoegen van het grafiektype.

Histogram

Maak een histogram van de eruptietijden via Invoegen > Aanbevolen grafieken > Alle grafieken > Histogram.

Experimenteer met Bin-breedtes van 2, 5, 10, 15, 30 en 50 sec.

Selecteer de X-as en kies daarna As opmaken > Bin-breedte > breedte invullen. Het venster met opties moet je meestal wat breder maken om de bin-breedte in te kunnen vullen!

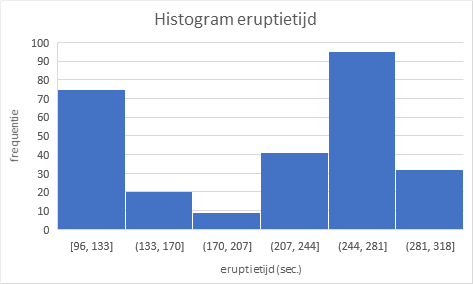
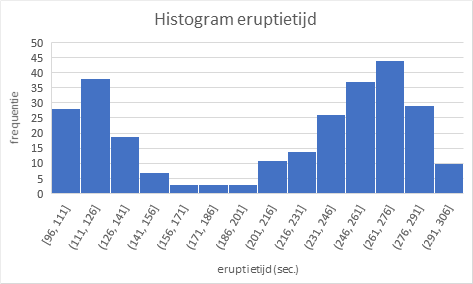
(a) standaarddiagram met een binbreedte van 37.

Bij wijziging van de Bin-breedte zie je de vorm van het histogram veranderen en ook de hoeveelheid informatie die je hieruit af kunt lezen. De zeer kleine bin-breedtes geven een wat rommeliger figuur en je ziet teveel details. Bij de grootste bin-breedte is alle informatie uit het histogram verdwenen en kun je de twee pieken niet meer waarnemen. Het is een kwestie van proberen en ervaring om een goede breedte te vinden.

Een bin-breedte van 15 lijkt hier redelijk geschikt. Het is niet goed mogelijk om de twee piekmomenten precies af te lezen. Wel kun je zien dat de eerste piek in het interval [111, 126] ligt en de tweede piek in het interval [261, 276].

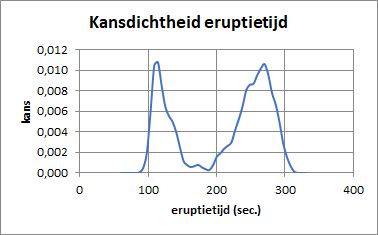
Bij theoretische verdelingen zoals de normale verdeling, kun je kansdichtheidsdiagrammen maken waardoor je veel meer details in de verdeling kunt zien. Helaas lijkt de verdeling van de eruptietijden niet op een van de bekende verdelingsfuncties.

Voor dergelijke situaties kun je als een goed alternatief een zogenaamde Kernel dichtheidschattingsdiagram maken, maar helaas wordt dit grafiektype niet door Excel aangeboden. Veel statistische add-ins ondersteunen dit grafiektype wel.

Figuur 7.17: Kernel dichtheidschatting, gemaakt met de addin van Real Statistics. De twee pieken komen hier duidelijker naar voren.

Een redelijk alternatief is een diagram met een cumulatieve empirische verdeling. Excel biedt deze mogelijkheid aan via de histogramopties van Gegevensanalyse. Normaliter moet je hiervoor eerst zelf een kolommetje bins maken met de intervalgrenzen, maar wanneer je dat niet doet en dus de bins niet specificeert, dan worden er bins gemaakt die waarschijnlijk wat minder optimaal zijn. Voor een eerste verkenning is dat geen probleem.

Maak nu opnieuw een histogram, maar nu via Gegevens -> Gegevensanalyse -> Histogram. Specificeer voor het invoerbereik de kolom met gegevens. Laat het Verzamelbereik leeg. Wanneer de eerste rij in het invoerbereik zit moet je ook Labels aanvinken. Selecteer bij de uitvoeropties Cumulatief percentage en Grafiek maken.

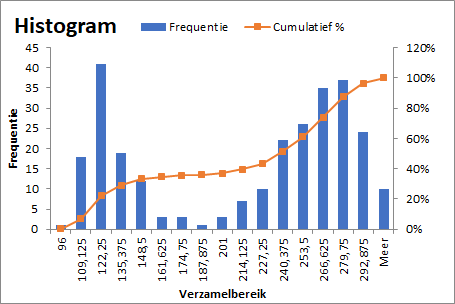
Figuur 7.18: Histogram met cumulatief percentages.

De procedure heeft hier een bin-breedte van 13,5 genomen, deze geeft net wat meer details dan bij de bin-breedte van 15. In de lijn voor de cumulatieve percentages zie je steilere hellingen aan de linkerkant van de piekmomenten die zo rond 120 sec. en 270 sec. liggen

7.7.2 Wachttijd

Voer gelijke opdrachten uit voor de variabele wachttijd.

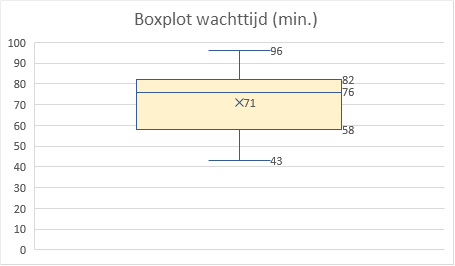
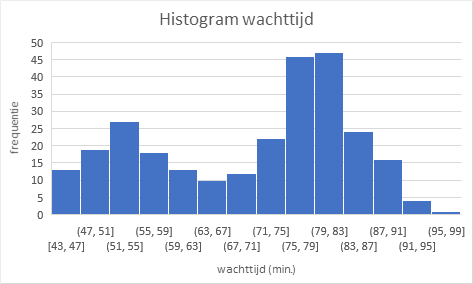
Figuur 7.19: Samenvattende statistieken wachttijd.

Figuur 7.21: Histogram wachttijd met een bin-breedte van 4.

Het overall beeld is gelijk aan dat van de eruptietijden: een links scheve verdeling. Ook hier twee pieken die in de buurt van 55 min. en 80 min. liggen.

7.7.3 Eruptietijd - Wachttijd

Spreidingsdiagram

Maak een spreidingsdiagram van eruptietijd (X-as) tegen wachttijd (Y-as).

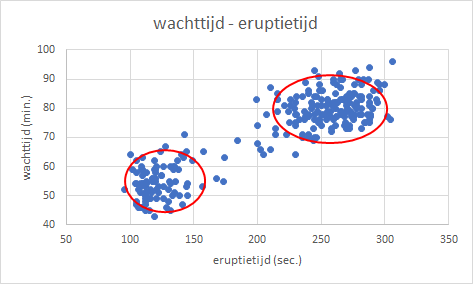
Je zie hier twee ellipsvormige clusters van punten die overeenkomen met waarnemingen in de buurt waar de twee laagste waarden van de pieken en de twee hoogste waarden van de pieken (270,80) samenkomen. Op het oog is een scheidingsgrens tussen deze twee clusters een eruptietijd van 180 sec. (3 minuten).

Om hier betekenis aan toe te kennen en/of vervolgvragen te formuleren is, zoals meestal, meer deskundigheid nodig over de context van het onderzoek.

7.8 Opgaven

Oefening 7.1 Kwartaalomzetten

Het bestand kwartaalomzet.csv bevat de kwartaalverkopen van vijf producten (A, B, C, D en E) over de jaren 2015 t/m 2020. De bedragen voor de omzet zijn in duizenden euro’s.

Maak een nieuw Excelbestand en laad het csv bestand in via Power Query. Geef de tabel als naam “omzetdata” en sla het Excelbestand op onder de naam “kwartaalomzet.xlsx”.
Bepaal met één draaitabel het gemiddelde, standaarddeviatie, maximum en minimum per produkt.
Maak een draaitabel met draaigrafiek van de omzet op een nieuw werkblad. De rijgegevens zijn de jaren en de kolomgegevens de kwartalen. De grafiek is een kolomdiagram. Bestudeer de grafiek. Wijzig daarna het kolomdiagram in een gestapeld kolomdiagram en bekijk de grafiek opnieuw. Ga voor jezelf na of deze grafieken je voldoende inzicht geven in de data, zoals bijvoorbeeld de onderlinge verschillen per kwartaal.
Maak opnieuw een draaitabel met draaigrafiek van de omzet op een nieuw werkblad, waarin jaar en kwartaal de rijgegevens vormen en de productsoorten de kolommen. De grafiek moet je wijzigen in een lijndiagram met markeringen. Bestudeer de tabel en grafiek. Welke zaken vallen je op?

Kijk eens naar de omzetten van product A per kwartaal. Zit daar veel variatie in? - Kijk eens naar de omzetten van product D per kwartaal. Zit daar veel variatie in?

Voeg een slicer toe waarmee je op productsoort kunt selecteren. Bestudeer achtereenvolgens de grafieken voor elk product en noteer de bijzonderheden.
Selecteer in de slicer de producten A en E en vergelijk het verloop van deze producten. Valt je iets op?

In de eerste drie jaren gaan hoge verkopen van A in de eerste twee kwartalen gepaard met lage verkopen van E. Ze lijken negatief gecorreleerd te zijn.

Oefening 7.2 Raddraaier

Het fietsenbedrijf Raddraaier dat fietsen, accessoires en kleding verkoopt in zes landen neemt in 2017 een nieuwe verkoopmanager aan. Om deze kennis te laten maken met het bedrijf, het productportfolio en de verkoopprestaties sinds 2011 wordt door de IT-afdeling het bestand raddraaier.xlsx aangeleverd dat de volgende gegevens bevat.

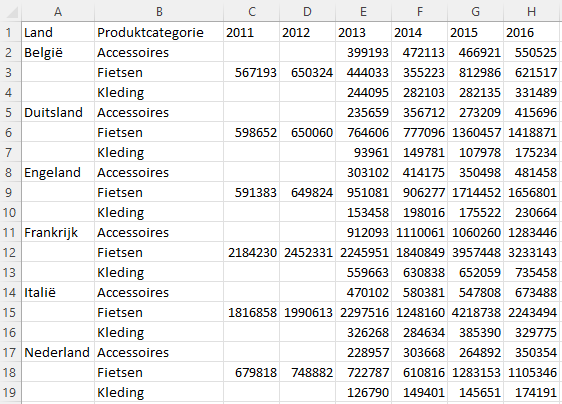
Verplaats je in de rol van deze verkoopmanager. Maak aan de hand van deze gegevens een eerste verkennende analyse. Denk hierbij bijvoorbeeld aan vragen als
- Wat zijn de ontwikkelingen voor elke productcategorie per jaar?
- Wat is het aandeel (percentage) van elke categorie in de totale omzet. Verschilt dit sterk per jaar?
- Wat is de omzet per land?
- Verkoopt elke categorie in elk land even goed?
- …

De vorm waarin de data is aangeleverd in het bestand raddraaier.xlsx is een kruistabel, welke niet echt geschikt is om bijvoorbeeld draaitabellen en draaigrafieken te maken voor de analyses. Hiervoor moeten de gegevens eerst gestructureerd worden. Dit kan als volgt:

Selecteer een cel met data. Kies Gegevens > Van tabel/bereik > OK.
In Power Query-editor selecteer kolom Land > R muisklik > Doorvoeren > Omlaag.
Selecteer de kolommen 2011 t/m 2016 > Transformeren > Draaitabel opheffen voor kolommen.
Wijzig de naam van de laatste twee kolomnamen in Jaar en Omzet.
Tab Start > Sluiten en laden.

De data wordt in een nieuw werkblad geladen en ziet er als volgt uit:

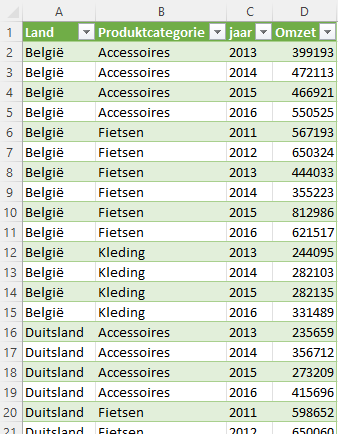
Figuur 7.24: Gestructureerde verkoopgegevens

Voor een verdere verdieping van de analyse heb je meer gedetailleerde gegevens nodig. Maak een lijstje met gegevens die de IT-afdeling voor jou moet aanleveren.

Oefening 7.3 Werknemers

Het bestand werknemers.xlsx bevat de persoonsgegevens van de werknemers van een bedrijf dat wereldwijd computers verkoopt. Maak een verkennende analyse aan de hand van de volgende vragen.

Hoeveel werknemers telt het bedrijf?
Hoe is de leeftijdsopbouw van de medewerkers?
Hoe is de opbouw van de diensttijd?
Bereken het aantal werknemers dat salarissen verdient in de klassen 0-1000, 1000-2000, 2000-3000, 3000-4000, 4000 en mee. Breng dit ook grafisch in beeld.
Herhaal vorige vraag, maar nu met een onderverdeling op geslacht.